Moteur à ondes de détonation pulsées - Définition
La liste des auteurs de cet article est disponible ici.
Initiation de la détonation
Deux mécanismes existent pour créer une détonation :
- l'initiation directe qui produit les détonations les plus « pures », mais qui nécessite une très grosse quantité d'énergie ;
- la transition déflagration-détonation ou DDT : cette initiation s'observe dans des mélanges très réactifs (acétylène/air, hydrogène/air). Les ondes de combustion accélèrent grâce au réchauffement des gaz imbrûlés en aval de l'onde provoqué par une succession d'ondes de compression liées à la dilatation des gaz brûlés. La température plus élevée des gaz imbrûlés augmente la vitesse du son, permettent ainsi aux différentes ondes de rattraper l'onde initiale. Cette accélération des gaz imbrûlés entraîne le développement de mouvements turbulents qui provoquent la distorsion du front de flamme qui se déchire peu à peu : plusieurs zones de réactions se forment et leurs mouvements relatifs créent d'importantes fluctuations de température et de concentration des constituants. Des cellules caractéristiques de la détonation se forment alors progressivement. Une contrainte de la DDT est d'avoir une longueur de tube suffisamment importante pour permettre à la transition de se développer. Une des approches les plus couramment utilisées actuellement consiste à utiliser une chambre séparée dans laquelle la DDT est initiée.
La purge du moteur
La phase de purge est importante pour déterminer la fréquence du moteur.
La détonation
Le principal mécanisme du PDE est la détonation. C'est pourquoi la connaissance de toutes ses caractéristiques est indispensable pour développer un moteur efficace.
Les modèles
Théorie de Chapman-Jouguet
C'est le modèle le plus simple de détonation, tiré notamment des travaux d'Emile Jouguet. Il suppose que la détonation est une simple discontinuité dans l'écoulement et que le taux de réaction chimique est infini. À partir de là, on peut établir des outils spécifiques aux ondes de détonation. Les équations de conservation s'écrivent :
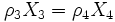
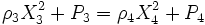
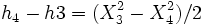
Ce système a une solution unique qui correspond à l'état de Chapman-Jouguet ; il définit une vitesse pour l'onde de détonation (UCJ) qui est égale à 1 ainsi que la composition des produits de combustion.
Modèle ZND
Il a été développé pendant la Seconde Guerre mondiale par Zeldovich, Neumann et Döring pour prendre en compte la vitesse de réaction chimique. Le modèle ZND décrit l'onde de détonation comme une onde de choc immédiatement suivie par une zone de réaction chimique (la flamme). L'épaisseur de cette zone est donnée par le taux de réaction. La théorie ZND donne la même vitesse de réaction et les mêmes pressions que la théorie Chapman-Jouguet mais prend en plus en compte l'épaisseur de l'onde.
Les détonations réelles
Les détonations sont en réalités des structures en trois dimensions comprenant des ondes de choc et des zones de réaction. Les ondes de chocs sont constitués de segments de courbes ; à chaque ligne de détachement, les ondes de choc interagissent sous forme de configurations de Mach. La taille de ce motif en forme d'écailles de poisson créé par les intersections d'ondes de choc est caractéristique du taux de réaction chimique du mélange et définit ainsi une échelle caractéristique de la cellule de réaction. La taille de ces cellules est un facteur limitant pour le diamètre du tube : une détonation ne peut pas se propager dans un tube de diamètre inférieur à la taille de cellule divisé par Pi, cette limite correspondant à des détonations hautement instables.
La propagation de la détonation
Les conditions aux limites
L'analyse de la dynamique des gaz requiert de connaître ce qui se passe quand l'onde de détonation incidente atteint l'extrémité ouverte du tube. Cette interface peut être modélisée en 1D comme une surface de contact. Quand l'onde de détonation atteint cette surface, une onde transmise va se propager vers l'extérieur du tube tandis qu'une onde réfléchie repart vers l'intérieur du tube. Dans le cas d'une détonation se propageant dans de l'air à une atmosphère, l'onde transmise sera toujours une onde de compression. L'onde réfléchie peut être de compression ou de détente. La façon la plus simple de déterminer sa nature est d'utiliser le diagramme Pression/Vitesse.
Analyse de la dynamique des gaz
La dynamique des gaz dans une tube idéal (c'est-à-dire sans obstacles) peut être analysée grâce au diagramme distance/temps. Ce diagramme x-t représente l'onde de détonation se propageant à la vitesse Chapman-Jouguet UCJ suivie par une onde de détente de Taylor. Est représentée aussi la première caractéristique réfléchie à l'interface gaz/air en sortie de tube. Cette caractéristique à une pente initiale déterminée par les conditions à l'interface qui est modifiée par l'interaction avec l'onde de Taylor. Une fois qu'elle a franchi cette onde de Taylor, la première caractéristique se propage à la vitesse du son dans le milieu c3. La région derrière cette première caractéristique est complexe car l'onde de détente réfléchie interagit aussi avec l'onde de Taylor.
Deux temps caractéristiques peuvent être définis : t1 correspondant à la réflexion de l'onde de détonation à l'interface externe et t2 correspondant au temps nécessaire à la première caractéristique réfléchie pour atteindre l'extrémité fermée.
La différence de pression sur cette surface de poussée entraîne l'impulsion spécifique d'un cycle simple. Il est donc intéressant de se focaliser sur l'historique en pression sur l'extrémité fermée. Quand la détonation est initiée, un pic de pression est enregistré (le pic de Chapman-Jouguet) puis la pression chute à P3 suite au passage de l'onde de Taylor. La pression sur la surface de poussée reste constante jusqu'à ce que la première onde réfléchie atteigne cette paroi. L'onde de détente réfléchie fait alors décroître la pression jusqu'à la valeur extérieure. Le pic de pression de Chapman-Jouguet se produit pendant un temps très court et ne participe donc pas à la poussée. La pression reste constante ensuite pendant un temps t1+t3 à la pression P3 calculée avec les équations de l'écoulement isentropique.
Calcul de l'impulsion spécifique
En reprenant la formule exposée plus haut :
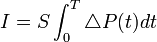
![I=S\cdot[\triangle P_3(t_1+t_2)+int_{t2}^{T}\triangle P(t)dt]](https://static.techno-science.net/illustration/Definitions/autres/3/31ae5b128ceca5efcbba36251cc602c7_f74b3a0e4ed55efaf299b76312008128.png)
Le temps t1 correspond au temps nécessaire à la détonation pour atteindre l'extrémité ouverte du tube de longueur L (
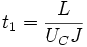
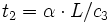
La dernière partie de l'intégrale de pression entre t2 et T est modélisé en introduisant un temps t3 exprimé à l'aide du paramètre &beta:
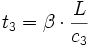
On peut donc réécrire l'impulsion sous la forme:
![I=S\cdot \triangle P_3\cdot [\frac{L}{U_CJ}+(\alpha+\beta)\cdot \frac{L}{c_3}]](https://static.techno-science.net/illustration/Definitions/autres/8/8825b7c730431bd632d6239df9253ab7_604059c3d887d392b86978b7f0e82273.png)
Le paramètre %alpha est déterminé par l'interaction de l'onde réfléchie et de l'onde de Taylor. Le paramètre %beta est calculé numériquement ou déterminé par expérimentation.

















































