Nomogramme - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Un nomogramme est un outil graphique de calcul constitué de courbes graduées entre lesquelles on place une règle. Le résultat de l'opération se lit au croisement de la règle et de l'une des courbes représentées en rouge dans les exemples ci-dessous. Le terme a été créé par Maurice d'Ocagne qui fut le principal promoteur de cette technique au début du XXe siècle.
Exemple
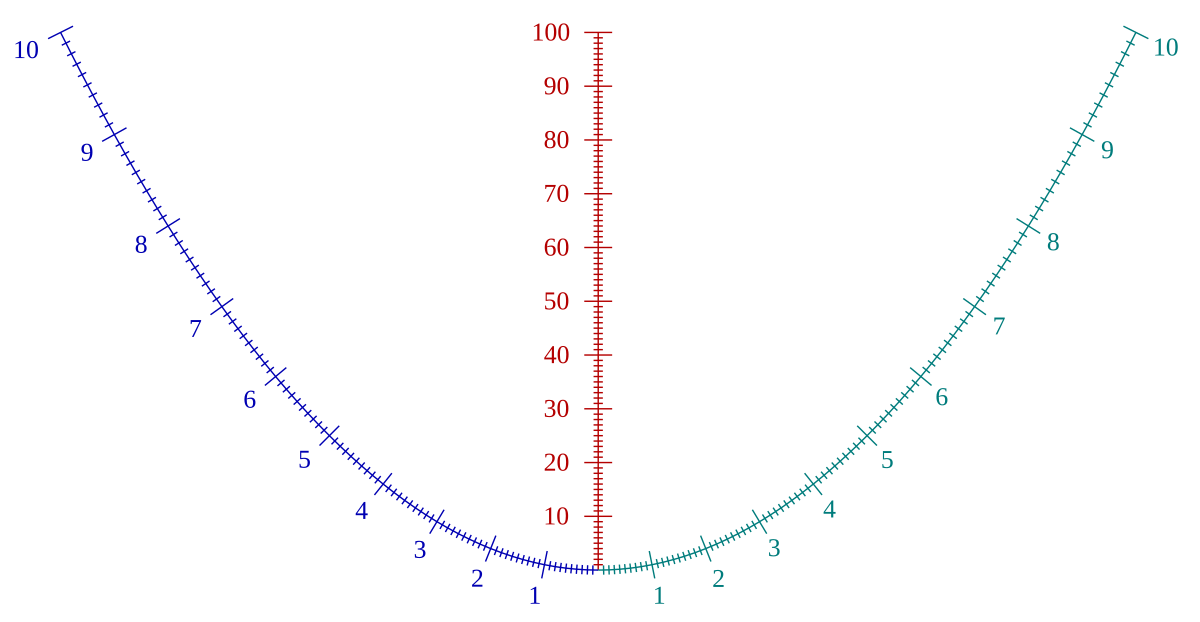
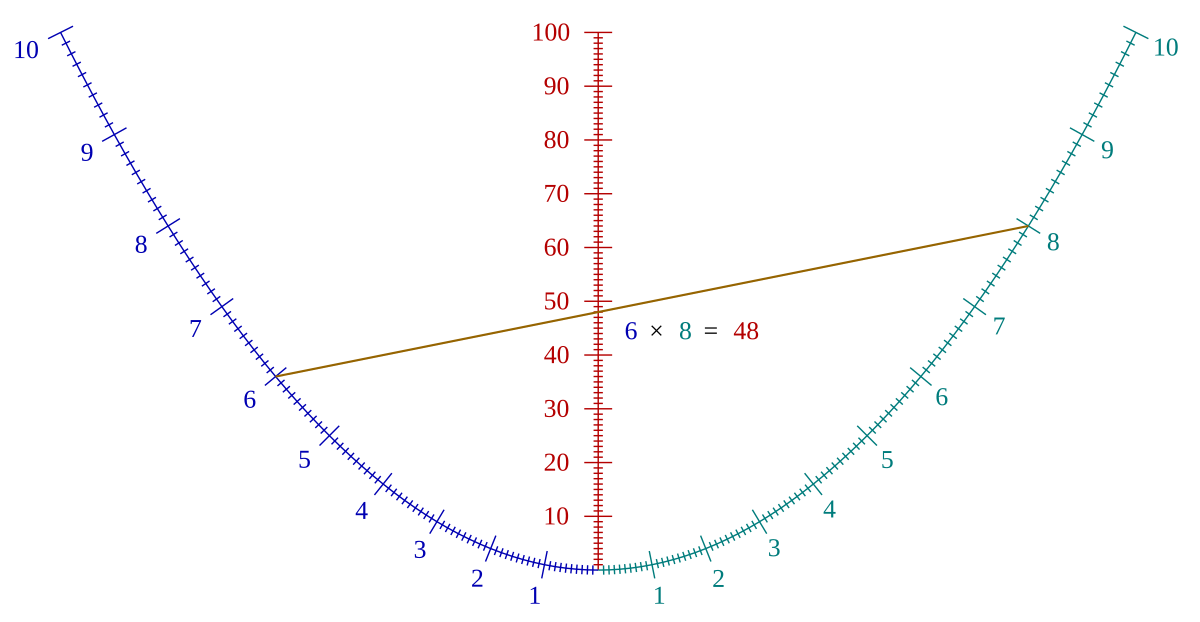
La parabole que voici est doublement cotée, ce qui veut dire qu'en fait on considère comme séparées les deux moitiés de celle-ci, graduées respectivement en bleu et en cyan. L'axe de la parabole, en rouge, est également gradué, mais les graduations ne vont plus jusqu'à 10 comme sur les deux branches latérales, mais jusqu'à 100.
Pour effectuer le produit de 6 par 8, il suffit de tirer un trait (ou pour conserver longtemps le nomogramme, poser une règle ou tendre un fil) entre la graduation 6 de la branche bleue et la graduation 8 de la branche cyan. Ci-contre le trait est en marron, et on voit qu'il coupe l'axe rouge sur la graduation 48, ce qui confirme que
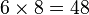
On peut manipuler ce nomogramme en ligne ici: [2].
Remarque historique
Plusieurs auteurs récents attribuent ce procédé de calcul à Yuri Matiyasevich, ce qui est impossible du point de vue de la chronologie (Matiyasevich a publié la recette du nomogramme en 1971). Il est très possible qu'à l'époque il ait ignoré les travaux de Clark, vu le peu de renommée de ceux-ci.
Autres exemples
Nomogramme à droites parallèles
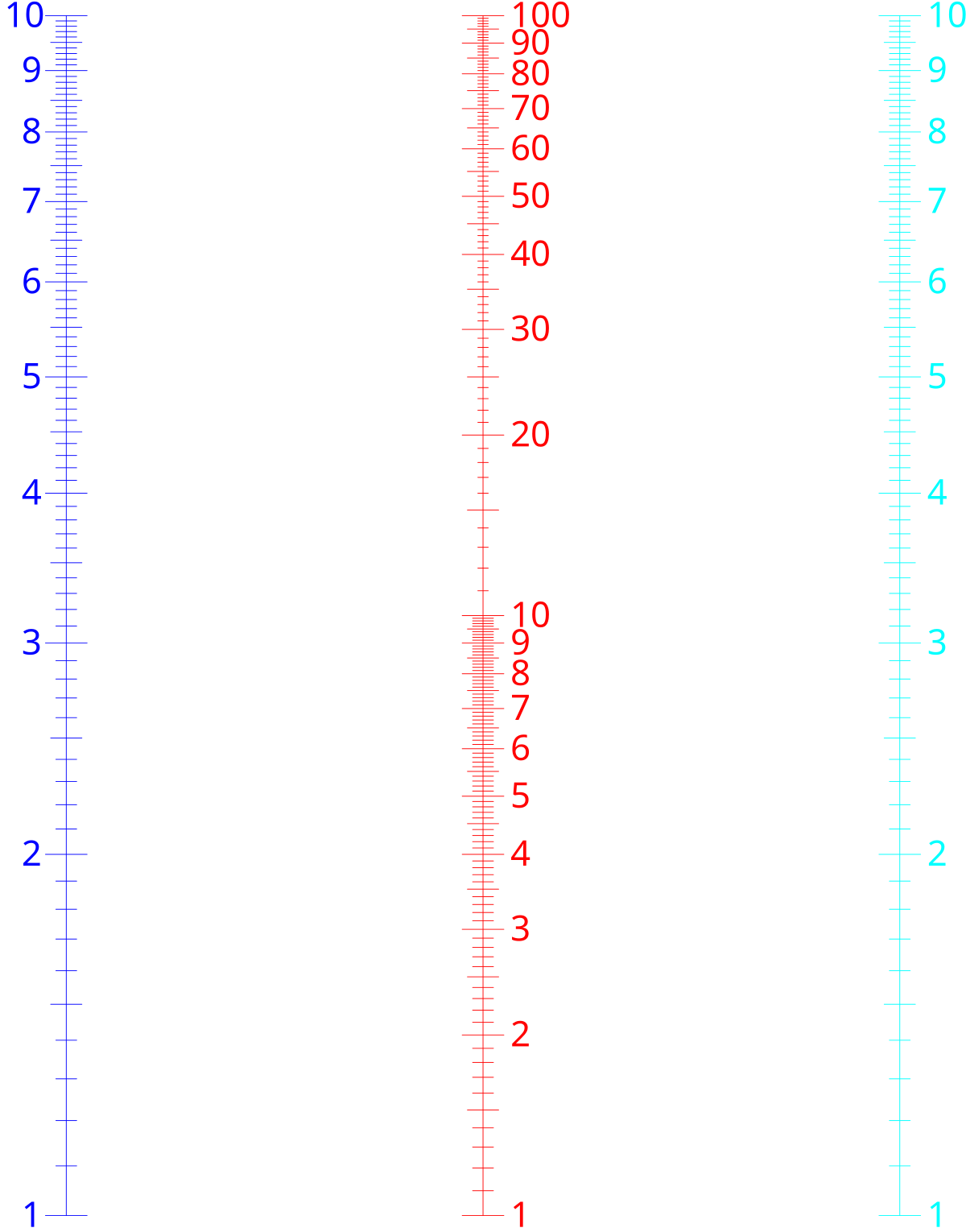
Le premier nomogramme publié par Maurice d'Ocagne est formé de droites parallèles.
Le principe de son utilisation est simple: On repère sur les droites extrêmes les deux facteurs à multiplier (graduations respectivement bleue et cyan) et on tire entre les deux, un trait rectiligne (de préférence matérialisé sous forme d'une règle ou d'un fil tendu pour ne pas laisser de marque sur le nomogramme).
Les graduations utilisent une échelle logarithmique et le principe du nomogramme est basé sur la conservation du milieu par projection.
On peut manipuler ce nomogramme en ligne ici: [3].
Nomogrammes de Clark
En 1907 et 1908, J. Clark, de l'école polytechnique du Caire, publia une série d'article où il expose l'utilisation par ses collègues de nomogrammes nouveaux. Il ébauche une théorie unificatrice de ces nomogrammes, qui utilisent des cubiques. En particulier, comme la parabole unie à son axe est une courbe cubique, la théorie de Clark explique le fonctionnement du nomogramme parabolique. Il l'étend à l'utilisation d'autres coniques.
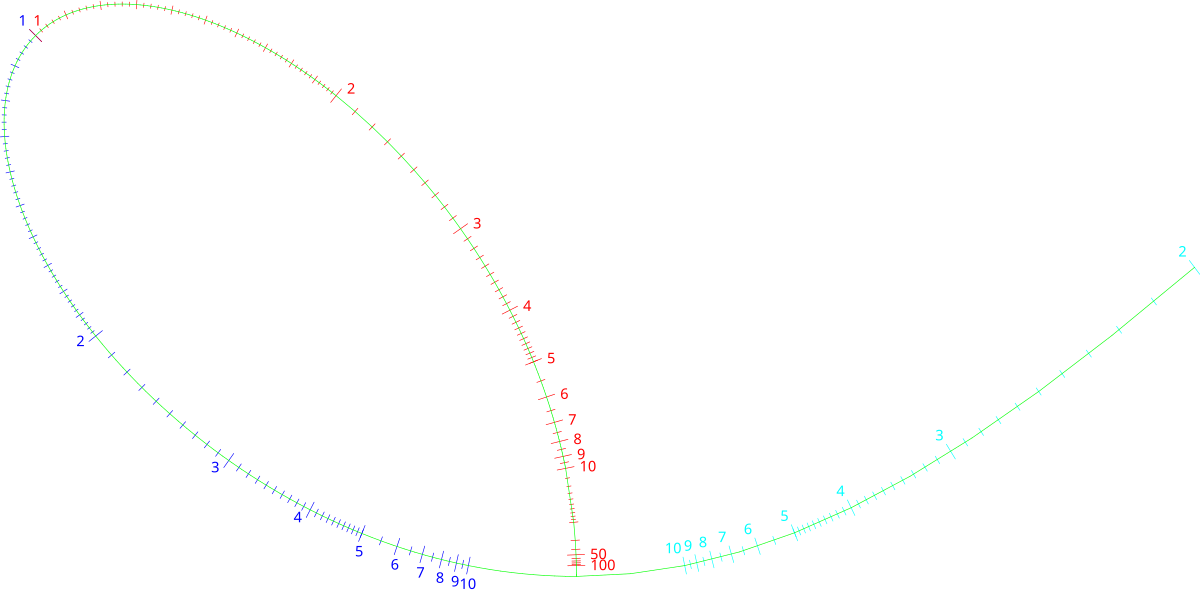
Nomogramme circulaire
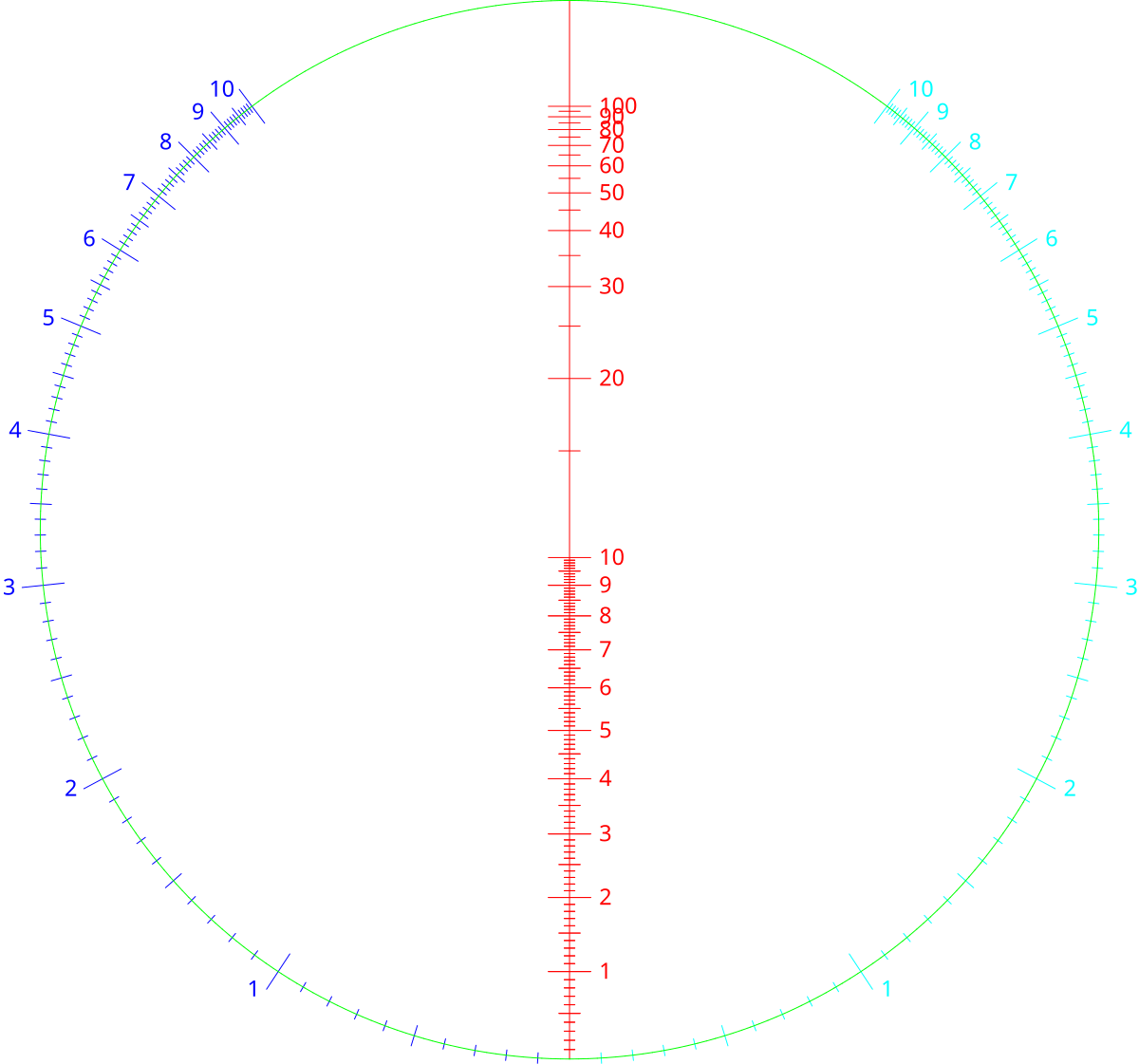
Le cercle est une conique, ce qui donne lieu à ce nomogramme de multiplication. Comme précédemment, les facteurs se lisent sur les graduations bleue et cyan, entre lesquelles on trace (virtuellement) un trait, et on lit le produit sur la graduation rouge qui est alignée avec ces deux graduations.
On peut manipuler ce nomogramme en ligne ici: [4].
Folium
Le folium est aussi une courbe cubique, ce qui a permis à Clark de construire une courbe à multiplier unique, où la même courbe porte les graduations des facteurs et celles du produit. Ce nomogramme fut présenté au congrès de Cherbourg en 1905, où il bénéficia d'un franc succès.
On peut manipuler ce nomogramme en ligne ici: [5].