Optimisation (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Notation
Les problèmes d’optimisation sont souvent exprimés avec une notation spéciale. Voici quelques exemples :
On cherche la valeur minimale pour l’expression x2 + 1, où x s’étend sur les nombres réels

On cherche la valeur maximale pour l’expression 2x, où x s’étend sur les réels. Dans ce cas, il n’y a pas de tel maximum puisque l’expression n’est pas bornée, donc la réponse est « l’infini » ou « indéfini ».
On cherche la ou les valeurs de x dans l'intervalle
![]-\infty, -1]](https://static.techno-science.net/illustration/Definitions/autres/1/1d6ab33b3fb95d1dab60c3aea17122a8_3b18df377ceec202a41334fe8005127f.png)
On cherche la ou les paires (x,y) qui maximisent la valeur de l'expression xcos(y), avec la contrainte ajoutée que la valeur absolue de x ne peut excéder 5. (À nouveau, la valeur maximale véritable de l'expression n'est pas importante.) Dans ce cas, les solutions sont les paires de la forme (5,2kπ) et ( − 5,(2k + 1)π), où k s'étend sur tous les entiers.
Historique
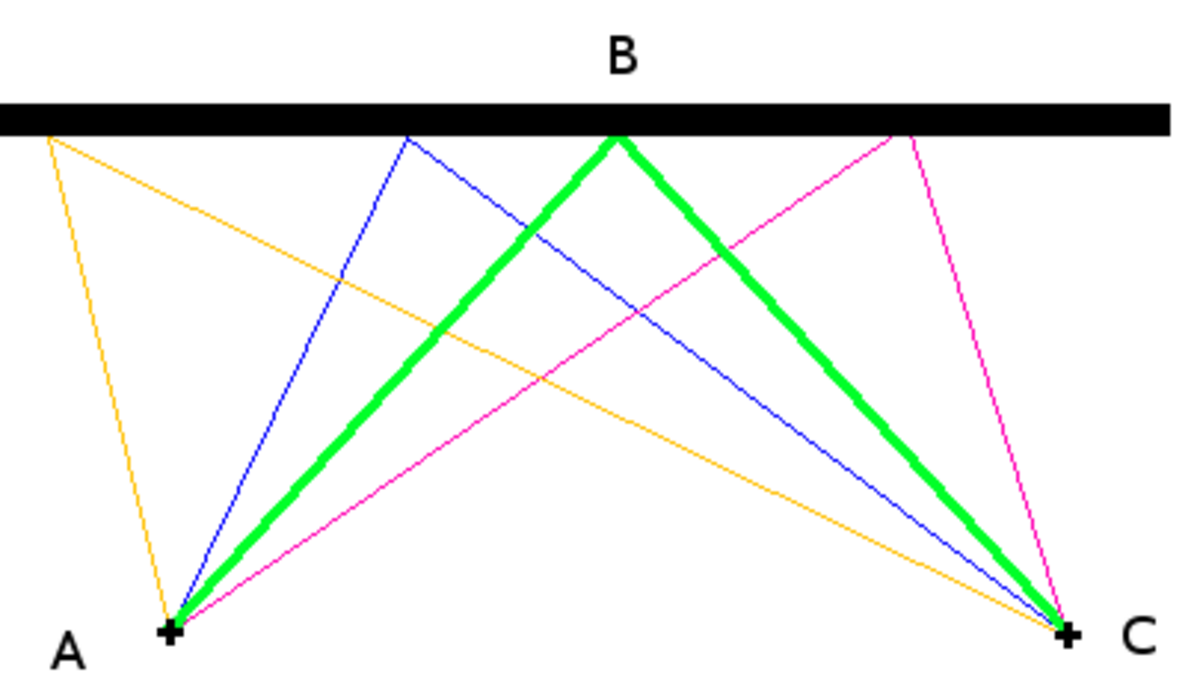
Les premiers problèmes d'optimisation auraient été formulés par Euclide, au IIIe siècle avant notre ère, dans son ouvrage historique Éléments. Trois cent ans plus tard, Héron d'Alexandrie dans Catoptrica énonce le principe du plus court chemin dans le contexte de l'optique. (voir figure)
Au XIIe siècle, l'apparition du calcul différentiel entraîne l'invention de techniques d'optimisation, ou du moins en fait ressentir la nécessité. Newton met au point une méthode itérative permettant de trouver les extrémums locaux d'une fonction en faisant intervenir la notion de dérivée, issue de ses travaux avec Leibniz. Cette nouvelle notion permet de grandes avancées dans l'optimisation de fonctions car le problème est ramené à la recherche des racines de la dérivée.
Durant le XVIIIe siècle, les travaux des mathématiciens Euler et Lagrange mènent au calcul variationnel, une branche de l'analyse fonctionnelle regroupant plusieurs méthodes d'optimisation. Ce dernier invente une technique d'optimisation sous contraintes: Les multiplicateurs de Lagrange.
Le XIXe siècle est marqué par l'intérêt croissant des économistes pour les mathématiques. Ceux-ci mettent en place des modèles économiques qu'il convient d'optimiser, ce qui accélère le développement des mathématiques. Depuis cette période, l'optimisation est devenue un pilier des mathématiques appliquées et le foisonnement des techniques est tel qu'il ne saurait être résumé en quelques lignes.
On peut tout de même évoquer l'invention plusieurs méthodes itératives utilisant le gradient de la fonction, ainsi que l'utilisation du terme programmation mathématique, pour désigner des problèmes d'optimisation. Historiquement, le premier terme introduit fut celui de programmation linéaire, inventé par George Dantzig dans les années 1940. Le terme programmation dans ce contexte ne réfère pas à la programmation informatique (bien que les ordinateurs soient largement utilisés de nos jours pour résoudre des programmes mathématiques). Il vient de l’usage du mot programme par les forces armées américaines pour établir des horaires de formation et des choix logistiques, que Dantzig étudiait à l’époque. L’emploi du terme « programmation » avait également un intérêt pour débloquer des crédits en une époque où la planification devenait une priorité des gouvernements.
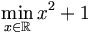
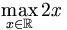
![\arg \min_{x \in ]-\infty, -1]} x^2 + 1](https://static.techno-science.net/illustration/Definitions/autres/b/b58195f0dd0ec89a6fcc2e54c1c249c9_e4f3947d33ff05b6936b9d9ac305a810.png)
![\arg \max_{x \in [-5, 5], y \in \mathbb{R}} x \cos(y)](https://static.techno-science.net/illustration/Definitions/autres/4/4881cbe7eef923ce6d71a8afc4f3abaf_5e4495f6b821d410b06aa5b090c1bcb7.png)