Optimisation (mathématiques) - Définition

Introduction

L'optimisation est une branche des mathématiques consistant à rechercher des conditions ou des configurations optimales pour des systèmes variés. Ce mot nous vient du latin optimum qui signifie le meilleur.

Elle est très importante en analyse numérique et dans les mathématiques appliquées, fondamentales pour l'industrie et l'ingénierie. En effet, lorsque un phénomène économique, physique, chimique... est exprimé par des équations, il est nécessaire d'optimiser le système afin d'obtenir un rendement maximal ou une configuration idéale. Pour cela on utilise des outils mathématiques. Aujourd'hui, tout est optimisé : Le fonctionnement d'un moteur, la gestion des lignes ferroviaires, les investissements économiques, les réactions chimiques... Les exemples sont multiples, il est donc crucial de posséder les outils pour résoudre ces problèmes.

Définition

Plus formellement, l'optimisation est l’étude des problèmes qui sont de la forme :

Étant donné : une fonction d’un ensemble A dans l'ensemble des nombre réels

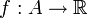
Rechercher : un élément x₀ de A tel que pour tous les x en A (« maximisation ») ou tel que pour tous les x en A (« minimisation »).

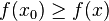
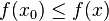
Une telle formulation est parfois appelée programme mathématique (terme non directement lié à la programmation informatique, mais utilisé par exemple pour la programmation linéaire - voir l’historique ci-dessous). Plusieurs problèmes théoriques et pratiques peuvent être étudiés dans cet encadrement général.

Étant donné que la maximisation de f est équivalente à la minimisation de − f, une méthode pour trouver le minimum (ou le maximum) suffit à résoudre le problème d'optimisation.

Il arrive fréquemment que A soit un sous-ensemble donné de l’espace euclidien , souvent spécifié par un ensemble de contraintes, des égalités ou des inégalités que les éléments de A doivent satisfaire. Les éléments de A sont appelées les solutions admissibles et la fonction f est appelée la fonction objectif. Une solution possible qui maximise (ou minimise, si c’est le but) la fonction objectif est appelée une solution optimale. Dans le cas particulier où A est un sous-ensemble de ou de , on parle d'optimisation combinatoire.

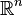
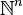
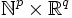
Un minimum local x ^* est défini comme un point tel qu'il existe un voisinage V de x ^* tel que pour tout ,  ; c’est-à-dire que dans un voisinage de x ^* toutes les valeurs de la fonction sont plus grandes que la valeur en ce point. Lorsque A est un sous-ensemble de , ou plus généralement un espace vectoriel normé, cela s'écrit : pour un δ > 0 donné et tous les x tels que on a . Les maximums locaux sont définis semblablement. En général, il est facile de trouver les minimums (maximums) locaux, qui sont parfois nombreux. Pour vérifier que la solution trouvée est un minimum (maximum) global, il est nécessaire de recourir à des connaissances additionnelles sur le problème (par exemple la convexité de la fonction objectif).

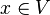
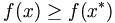
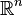
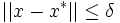
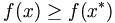
Techniques

Les techniques pour résoudre les problèmes mathématiques dépendent de la nature de la fonction objectif de l'ensemble contraint. Les sous-domaines majeurs suivants existent :

• la programmation linéaire étudie les cas où la frontière de l’ensemble A et la fonction objectif sont linéaires. C’est une méthode très employée pour établir les programmes des raffineries pétrolières, mais aussi pour déterminer la composition la plus rentable d’un mélange salé, sous contraintes, à partir des prix de marché du moment.
• la programmation linéaire en nombres entiers étudie les programmes linéaires dans lesquels certaines ou toutes les variables sont contraintes à prendre des valeurs entières. Ces problèmes peuvent être résolus par différentes méthodes : séparation et évaluation, plans sécants.
• la programmation quadratique permet à la fonction objectif d’avoir des termes quadratiques, tout en conservant une description de l’ensemble A à partir d'égalités/inégalités linéaires
• la programmation non-linéaire étudie le cas général dans lequel l’objectif ou les contraintes (ou les deux) contiennent des parties non-linéaires
• la programmation stochastique étudie le cas dans lequel certaines des contraintes dépendent de variables aléatoires
• la programmation dynamique utilise la propriété qu’une solution optimale se compose nécessairement de sous-solutions optimales (attention : le contraire n'est pas vrai en général) pour décomposer le problème en évitant l’explosion combinatoire. Elle n’est utilisable que lorsque la fonction objectif est monotone croissante. C’est la programmation dynamique qui permet par exemple
  • aux avionneurs de trouver les plans de décollage optimaux de leurs engins,
  • aux ingénieurs de bassin de répartir la production minière entre leurs différents puits
  • aux media planners de répartir efficacement un budget de publicité entre différents supports

Pour les fonctions dérivables deux fois, des problèmes sans contraintes peuvent être résolus en trouvant les lieux où le gradient de la fonction est 0 (par exemple les points stationnaires) et en utilisant la matrice hessienne pour classer le type de point. Si le hessien est défini positif, le point est un minimum local ; s’il est un défini négatif, un maximum local et s’il est indéfini c’est un « point-col ».

Si la fonction est convexe sur l’ensemble des solutions admissibles (définies par les contraintes) alors tout minimum local est aussi un minimum global. Des techniques numériques robustes et rapides existent pour optimiser des fonctions convexes doublement dérivables. En dehors de ces fonctions, des techniques moins efficaces doivent être employées.

Les problèmes à contraintes peuvent souvent être transformés en des problèmes sans contraintes à l’aide du multiplicateur de Lagrange : cette méthode revient en effet à introduire des pénalités croissantes à mesure qu’on se rapproche des contraintes. Un algorithme dû à Hugh Everett permet de mettre à jour de façon cohérente les valeurs des multiplicateurs à chaque itération pour garantir la convergence. Celui-ci a également généralisé l'interprétation de ces multiplicateurs pour les appliquer à des fonctions qui ne sont ni continues, ni dérivables. Le lambda devient alors juste un coefficient de pénalité.

De nombreuses techniques existent pour trouver un bon minimum local dans les problèmes d’optimisation non-linéaires avec plusieurs minimums locaux pauvres, elles sont généralement considérées comme des métaheuristiques.