Perspective isométrique - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La perspective isométrique est une méthode de représentation en perspective dans laquelle les trois directions de l'espace sont représentées avec la même importance, d'où le terme.
C'est un cas particulier de perspective axonométrique.
Principe
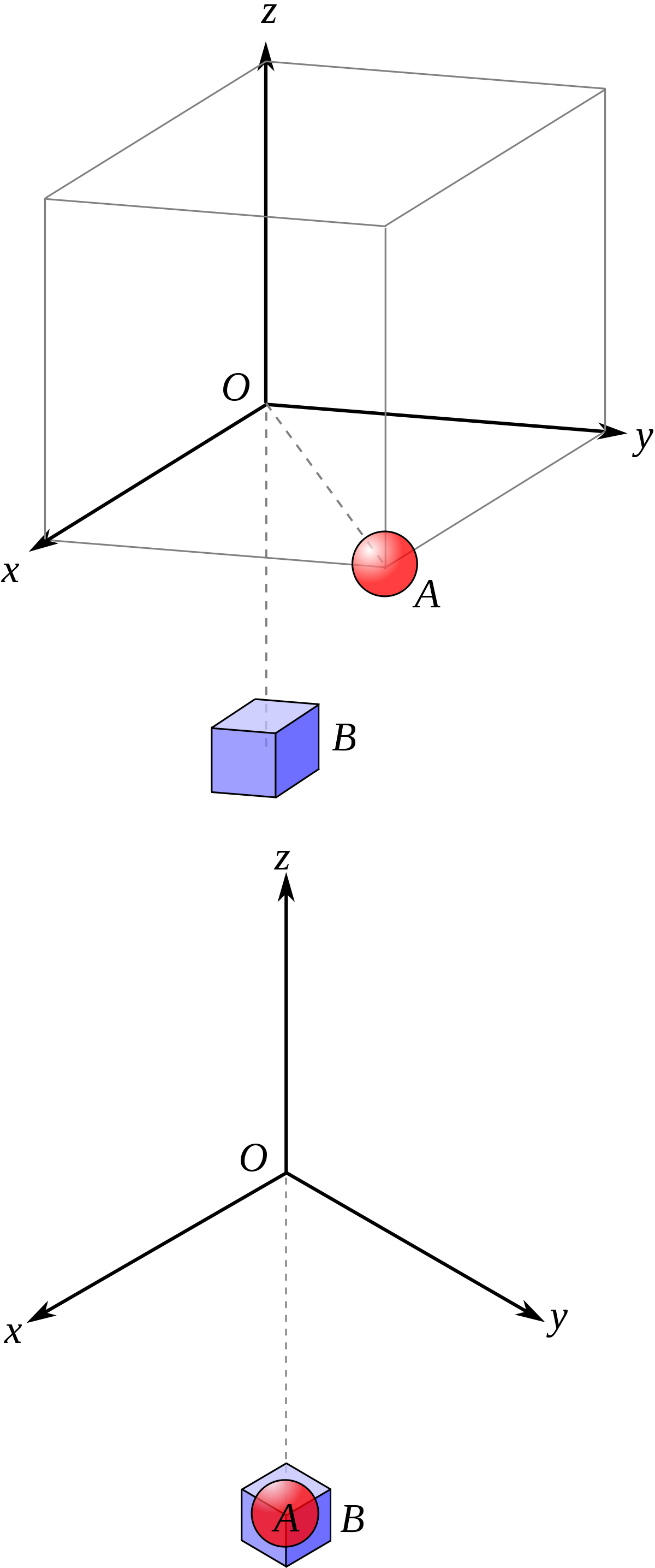
En géométrie analytique, on définit un repère orthonormé.
La perspective isométrique correspond à une vue selon la droite de vecteur directeur (1, 1, 1) dans ce repère. Ainsi, un cube dont les arêtes suivent les axes du repère se voit selon sa grande diagonale, comme un hexagone.
Les axes se projettent donc sur un plan perpendiculaire à cette grande diagonale. Les longueurs subissent une réduction (la projection est une isométrie, le facteur de réduction est le même pour toutes les longueurs sur un axe donné).
C'est une perspective qui est facile à exécuter dans le cas de formes simples. C'est une approximation de la vue « réelle », qui est satisfaisante tant que la profondeur reste faible : en particulier elle ne prend pas en compte la réduction apparente de taille avec l'éloignement.
Défauts et limites de la perspective isométrique
Comme toutes les projections et toutes les perspectives, la perte de la troisième dimension induit des erreurs possibles d'interprétation. Ceci a été abondamment utilisé par l'artiste M. C. Escher pour créer des situations impossibles.
En l'occurrence, un déplacement de 1 cm sur l'axe z se traduit graphiquement de la même manière qu'un déplacement de 1 cm selon l'axe des x et des y, soit un déplacement de √2 ≈ 1,41 selon la « diagonale » de (x, y).
Règles de base pour dessiner en perspective isométrique
Les mesures
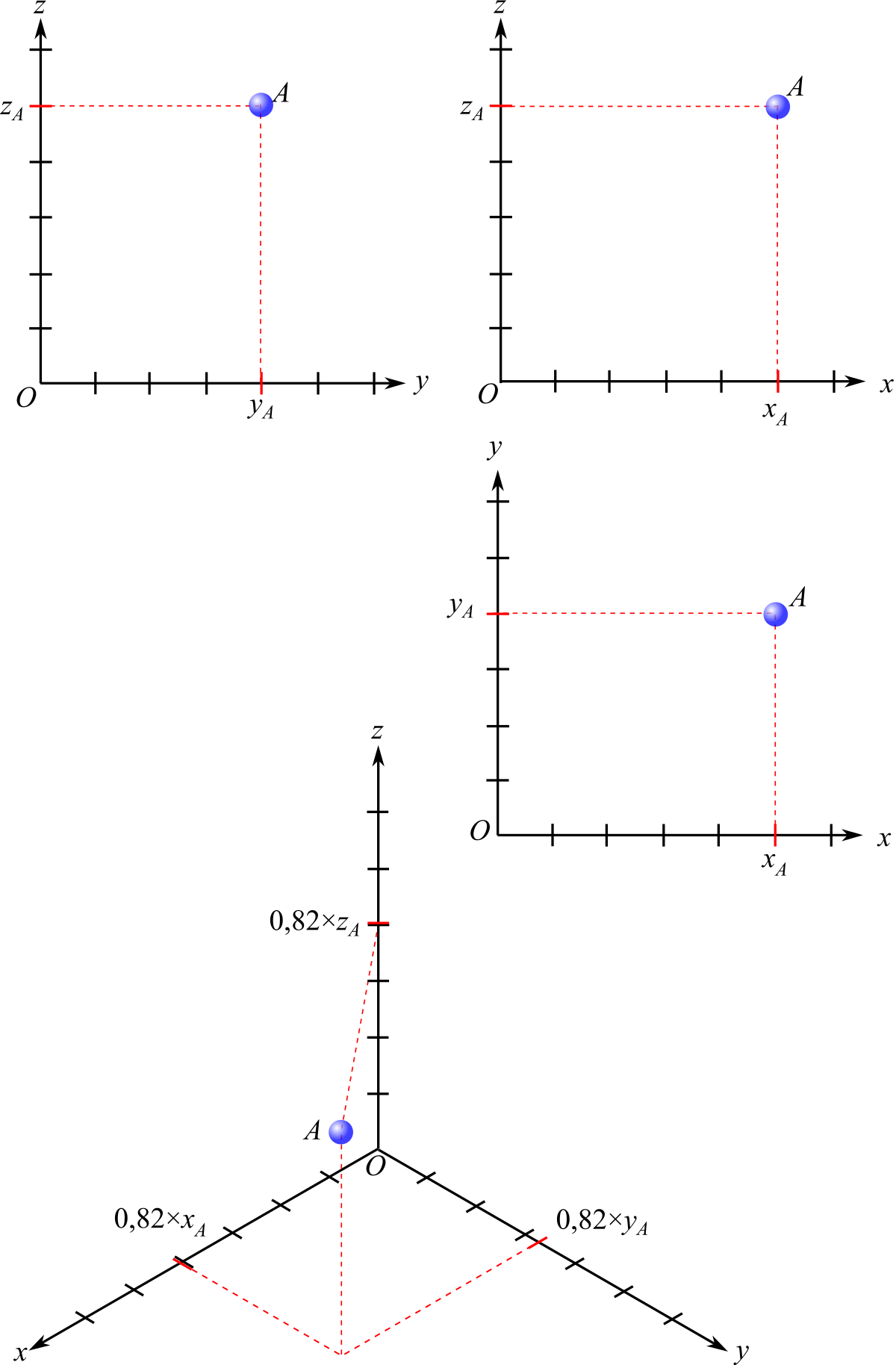
On parle de perspective isométrique car les distances sont reportées de la même manière sur les trois axes. On applique à toutes les longueurs qui sont colinéraires à un axe un coefficient réducteur de 0,82.
Dans le cas de la représentation d'un objet, on définit d'abord une face de l'objet que l'on considère comme la face avant, et l'on y place un repère ; dans ce plan, on n'a donc que deux axes visibles, le troisième est perpendiculaire au dessin. L'origine du repère est en général placée dans un coin.
On réalise ensuite deux vues (au moins) qui sont les projections orthogonales de l'objet sur la face avant et sur une face perpendiculaire (face de gauche, de droite, du dessus ou du dessous). Ensuite, il suffit de mesurer les coordonnées des points dans ce repère à partir des deux figures, et de reporter ces coordonnées sur les axes de la perspective isométrique en appliquant ce coefficient de 0,82.
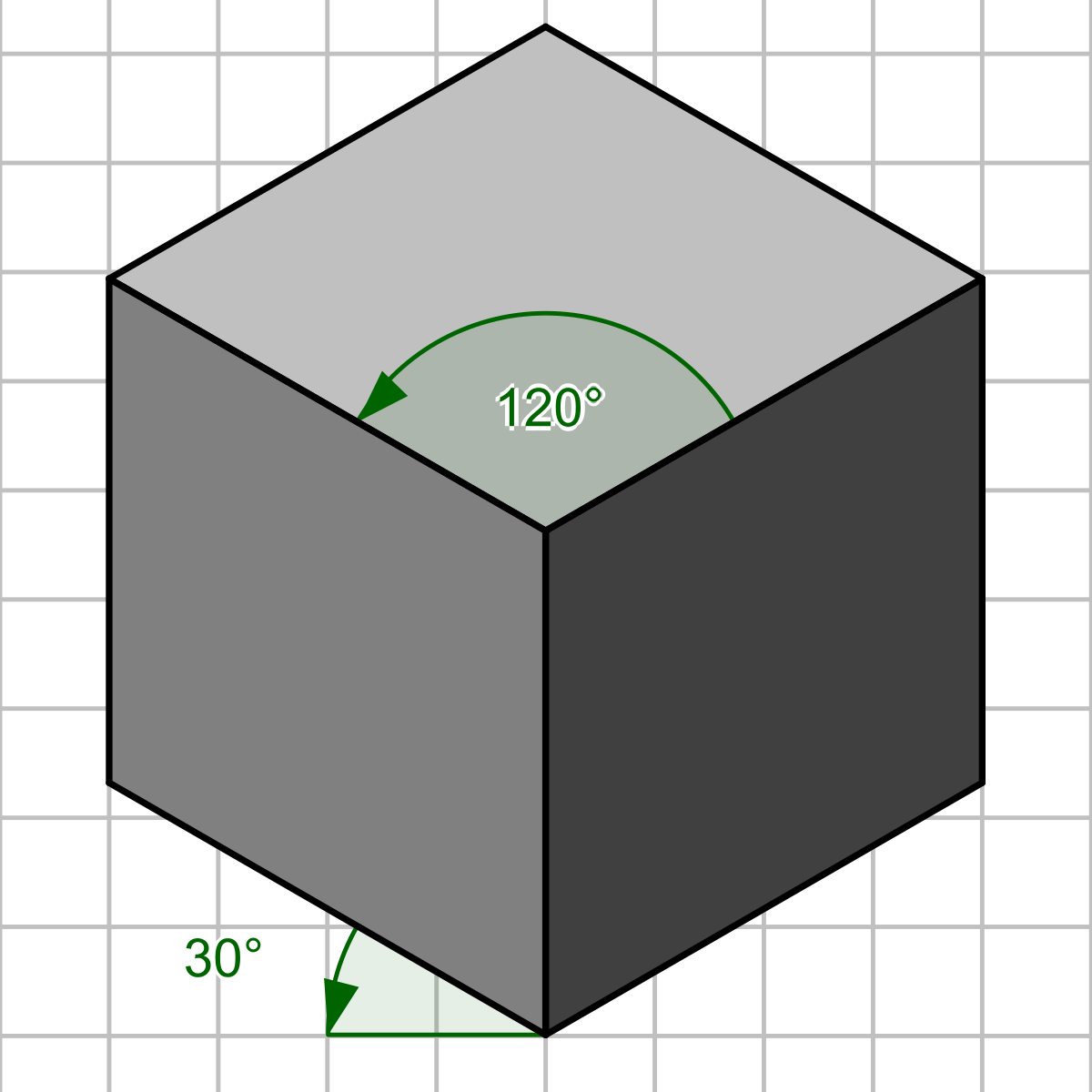
Les angles
Les angles entre les axes (x, y et z) sont tous égaux (120°).
Les cercles
Les cercles sont des formes importantes dans le dessin technique ; ceci est une conséquence des procédés de fabrication des pièces (usinage) : perçage, fraisage, tournage… Ils sont aussi importants en génie civil (débouchés de tuyaux, arc en plein-cintre, giratoires…). Lorsque l'on génère la perspective isométrique par ordinateur, celui-ci peut calculer la transformation du cercle. Mais ceci devient compliqué lorsque l'on dessine à la main.
Remarquons dans un premier temps qu'un cercle est toujours inscrit dans un carré auquel il est 4 fois tangent, au milieu des côtés. En vue de face, on contraint donc le cercle dans un carré.
En perspective isométrique, ce carré devient un parallélogramme. Les tangences restent les mêmes (milieu des côtés), mais le cercle devient une ellipse.
La projection oblique fait varier le diamètre du cercle entre 1 (grand diamètre de l'ellipse, donc diamètre horizontal du cercle de départ projeté en vraie grandeur) et 0,58 (son petit diamètre, vu sous sa plus importante réduction dans la direction de la plus grande pente).
Des trace-ellipses normalisés permettent de tracer des ellipses respectant ces proportions pour plusieurs tailles de grand axe.