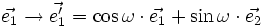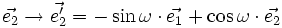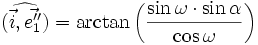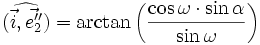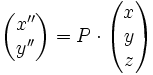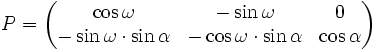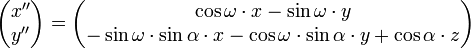Perspective axonométrique - Définition

Introduction

Dans un certain nombre de situations, et notamment en dessin technique, le dessin est la représentation d'objets réels. Le lecteur du dessin doit pouvoir se représenter la pièce en volume à partir de sa représentation sur papier, en deux dimensions. Se pose alors le problème du passage trois dimensions → deux dimensions, qui est notamment le domaine de la perspective.

Dans l'espace, on peut choisir un point de référence et trois règles graduées ayant des directions distinctes (on les choisit en général perpendiculaires) et non coplanaires (c'est-à-dire que les trois règles ne sont pas dans le même plan). On peut alors repérer un point de l'objet à dessiner (par exemple un sommet) par trois nombres, appelés « coordonnées », qui sont la distance à parcourir selon les trois directions pour aller du point de référence au point visé.

Voir l'article Repérage dans le plan et dans l'espace.

Une perspective axonométrique est un dessin sur lequel :

• les trois axes de référence sont représentés par trois droites ;
• les longueurs mesurées sur les règles graduées (les coordonnées) sont reportées avec un facteur constant pour chacune des droites (mais ce facteur peut être différent d'une droite à l'autre).

Ainsi, le dessin est particulièrement simple à réaliser, que ce soit à la main ou par calcul informatique (infographie, dessin assisté par ordinateur, synthèse d'image 3D).

Perspective axonométrique et vision réelle

La vision réelle est mieux rendue avec une perspective conique. Avec les perspectives axonométriques, l'éloignement par rapport à l'observateur se traduit uniquement par un déplacement dans le plan. Il n'y a en particulier pas de diminution de taille des objets avec l'éloignement. Par contre, si l'objet représenté est peu profond, l'effet de rapetissement est peu important, une perspective axonométrique peut donc donner une bonne illusion de ce que verrait l'œil.

Tout le problème consiste à choisir des directions et des rapports qui rendent un dessin facilement interprétable par le lecteur — on s'imagine bien qu'en prenant des axes et des rapports au hasard, on obtiendrait un dessin peu « réaliste ».

Défauts des perspectives axonométriques

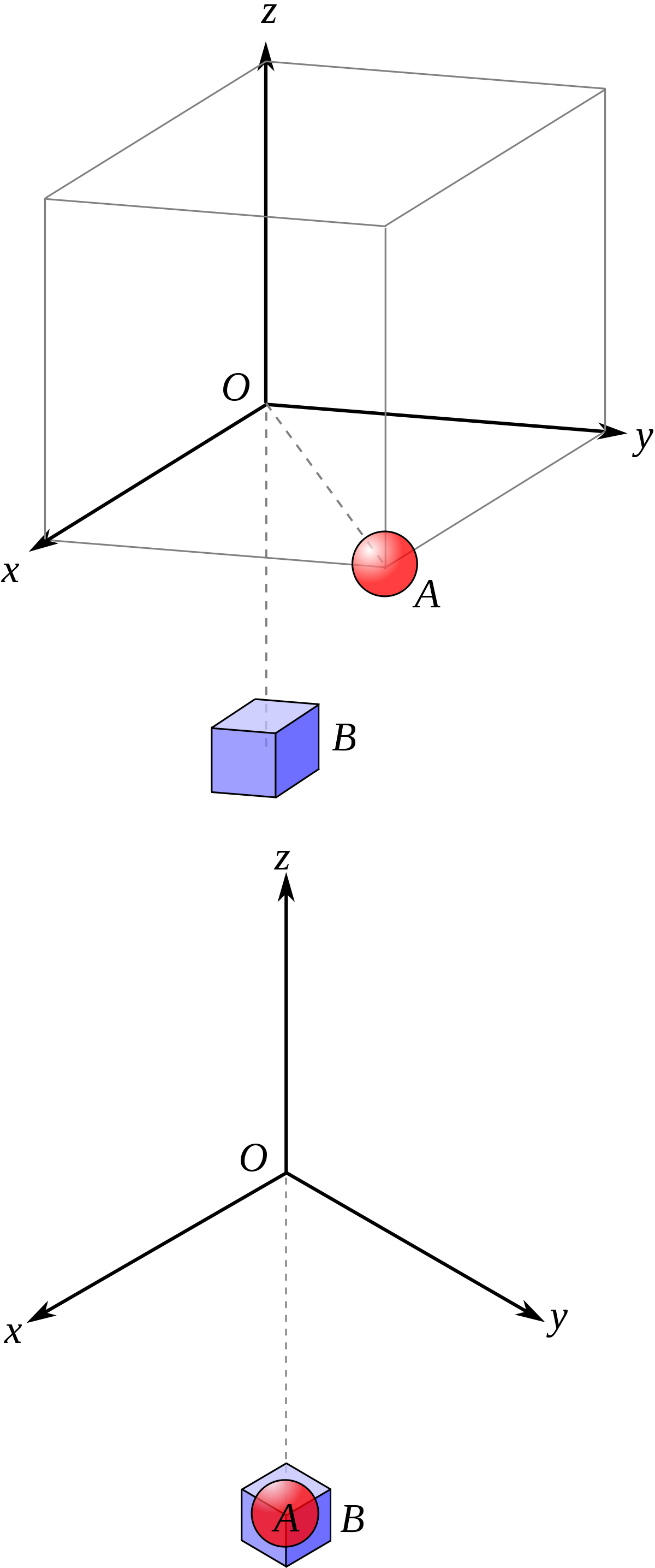
Comme toutes les projections et toutes les perspectives, la perte de la troisième dimension induit des erreurs possibles d'interprétation. Ceci a été abondamment utilisé par l'artiste M. C. Escher pour créer des situations impossibles.

Perspective axonométrique et arts plastiques

La peinture chinoise a beaucoup utilisé le dessin sans rapetissement avec l'éloignement. S'il ne s'agit pas de « construction à la règle », la notion est similaire.

Projections orthogonales

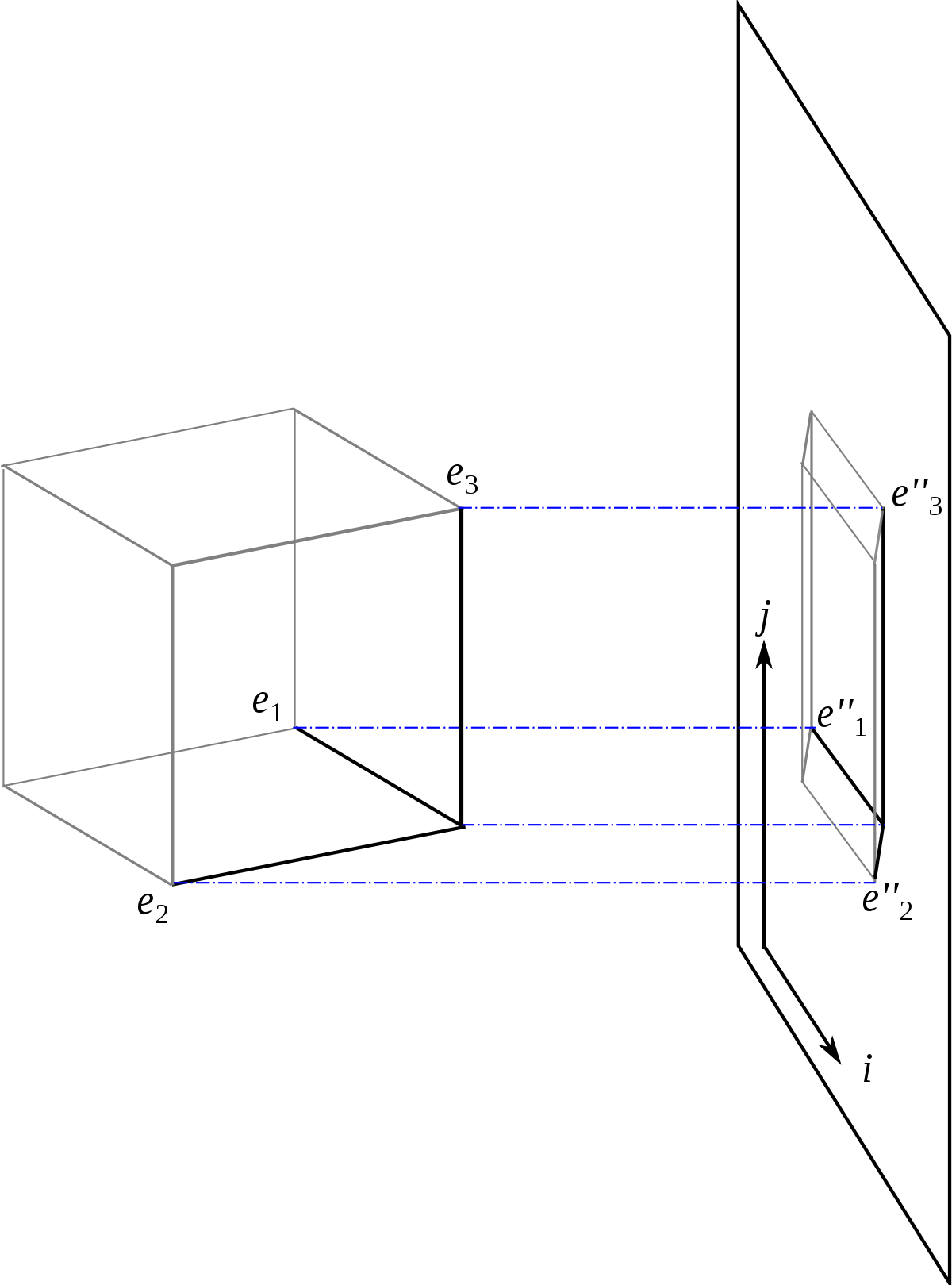
La projection orthogonale est une opération mathématique. Dans le cas qui nous intéresse, il s'agit de projeter un point de l'espace sur un plan, perpendiculairement à ce plan.

Par exemple, l'ombre créée par le Soleil, lorsque celui-ci est à la verticale de l'endroit où l'on se trouve, est une projection orthogonale de l'objet.

Les projections orthogonales sont des applications linéaires, ce qui signifie entre autres que deux vecteurs proportionnels restent proportionnels une fois projetés ; ce sont donc bien des perspectives axonométriques.

Si la projection peut se gérer simplement en infographie, la détermination des directions des axes projetés et des coefficients de proportionnalité pour le tracé manuel n'est pas très simple dans le cas général. On utilise de fait fréquemment des perspectives dimétriques pour lesquelles deux des coefficients sont égaux.

Détermination des directions des axes et des rapports

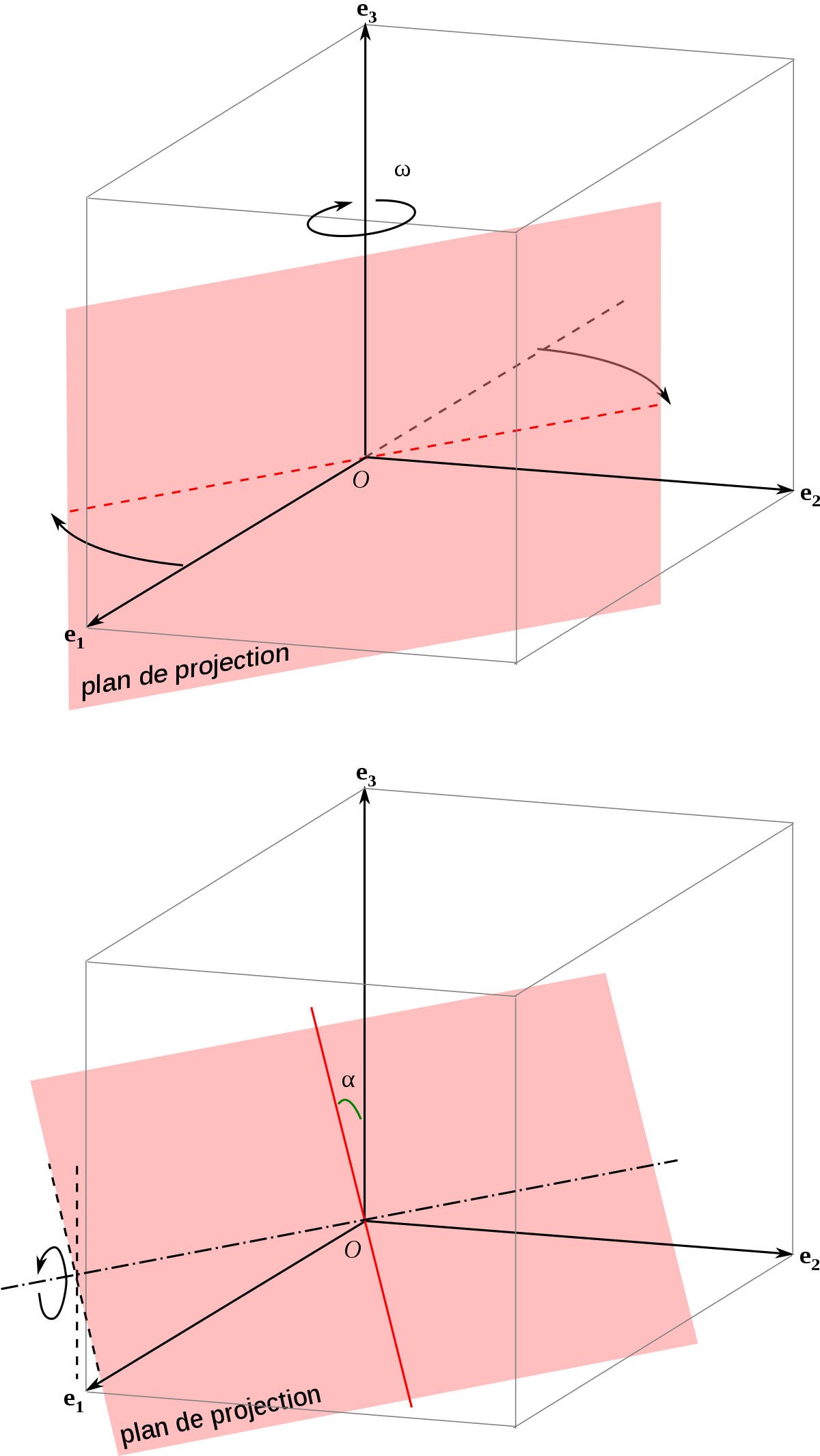
On peut décrire le plan de projection par des rotations transformant un plan donné, par exemple le plan (Oxz). Si l'on s'impose que la projection de reste verticale, alors on voit que le plan de projection peut s'obtenir par deux rotations, par exemple :

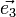
1. une rotation autour de l'axe (Ox) ;
2. puis une rotation autour de la projection de (Oz) sur le plan.

On peut aussi procéder dans « l'ordre inverse » :

1. une rotation autour de (Oz) ;
2. puis une rotation autour de la trace du plan (Oxy) sur le plan de projection.

Voir aussi l'article Angles d'Euler.

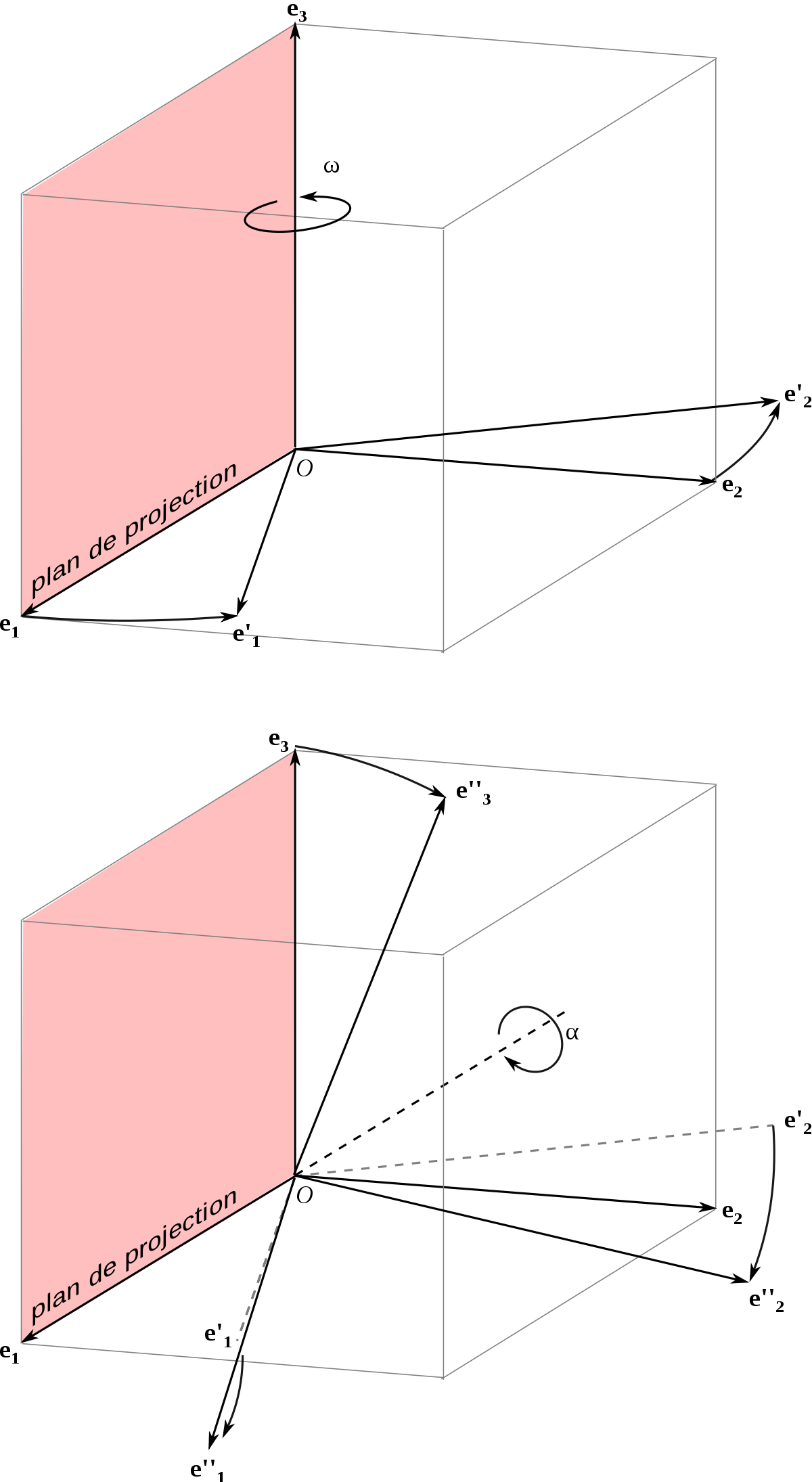
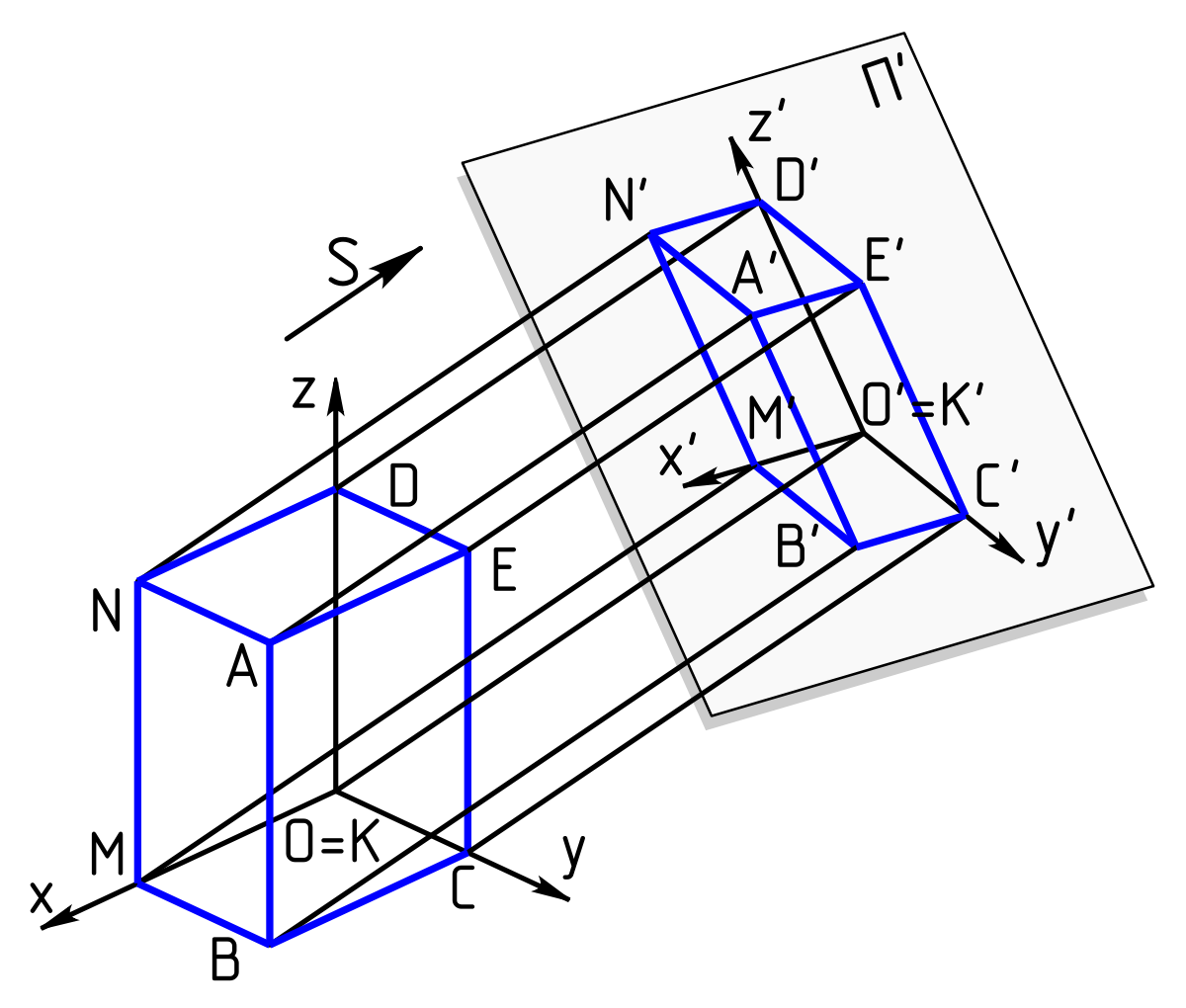
C'est cette deuxième manière de faire que nous allons retenir. Remarquons que l'on obtient le même résultat en considérant que le plan de projection reste fixe, mais que c'est le repère qui tourne (avec des angles opposés). Considérons que le plan de projection est (Oxz). Si l'on opère une rotation autour de (Oz) d'un angle ω, les vecteurs de la base se transforment en :

Si l'on applique ensuite une rotation d'angle α autour de l'axe Ox initial (qui est bien la trace de (Oxy) sur le plan de projection) puis que l'on fait la projection sur le plan, on voit que, étant le repère orthonormé direct du plan de projection (transformé de par les rotations si c'est le plan qui tourne, ou bien originel si c'est le repère qui tourne) :

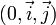
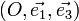
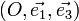
• le vecteur se projette selon  ;
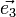
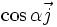
• le vecteur se projette comme lui-même ;
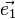
• la projection du vecteur est .

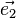
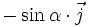
Les projections axes sont donc données par les vecteurs suivants, dont la norme est le coefficient de report :

• Ox :  ;
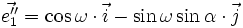
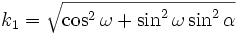
• Oy :  ;
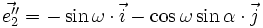
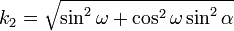
• Oz :  ; k₃ = | cosα |

Les angles des axes projetés et par rapport à l'horizontale peuvent se calculer à l'aide de la trigonométrie, par exemple :

• 
• 

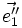
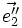
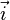
les angles étant ici non orientés.

Si x, y et z sont les coordonnées d'un point de l'espace dans le repère , et x" et y" les coordonnées de son projeté dans le repère , on peut définir la matrice P de la projection telle que

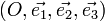
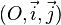
(voir l'article Produit matriciel), avec

et

Par exemple, pour ω = 30° et α = 20°, on a :

• k₁ ≈ 0,88 ;
• k₂ ≈ 0,58 ;
• k₃ ≈ 0,94 ;
• (i, e"₁) ≈ 11,17°
• (i, e"₂) ≈ 30,64°
• x" ≈ 0,87·x - 0,50·y ;
• y" ≈ -0,17·x - 0,30·y + 0,94·z.