Particule virtuelle - Définition

Introduction

En physique, une particule virtuelle est une particule dont les effets ne sont pas repérables, ni directement, ni indirectement mais dont l'existence est liée à l'explication de certains mécanismes fonctionnels. Elle est le résultat d'une démarche déductive imaginaire pour combler un manque théorique. Le superpartenaire en supersymétrie en est un exemple. Dans la théorie de la gravitation quantique à boucles, cette particule virtuelle s'associe à un fermion pour décrire le quantum de temps. Sa durée de vie est donc limitée à ce quantum dans l'espace associé. Même si elle reste imaginaire son existence est parfaitement définie au sein d'une pseudo-réalité virtuelle. C'est, jusqu'à présent le cas du boson de Higgs.

Particules virtuelles et fluctuations du vide

On pourrait définir simplement une particule virtuelle comme suit : particule ayant une courte durée d'existence.

L'expression « courte durée » est relative. L'important est que la particule apparaît, existe un certain temps sans être observée (sans interaction), puis disparaît (voir Vide quantique).

Le fait que des particules puissent être créées ou détruites est un fait acquis de longue date. Ce phénomène est maintenant largement observé dans les accélérateurs de particules où la collision de deux électrons, par exemple, peut donner lieu à l'émission de gerbes de nombreuses particules, certaines beaucoup plus massives que les électrons initiaux.

Ce phénomène est une conséquence du mariage de la relativité et de la mécanique quantique.

La relativité affirme que la masse est une forme d'énergie via la relation E = mc². Et l'on sait que les différentes formes d'énergie peuvent se convertir les unes dans les autres. On sait par ailleurs qu'une partie de la masse d'un noyau peut se convertir en énergie via les phénomènes de fission ou de fusion nucléaires.

D'un autre côté, le principe d'incertitude nous dit qu'en mécanique quantique certaines variables ne peuvent être connues avec une précision arbitraire. Plus exactement, certaines paires de variables dites conjuguées ne peuvent être connues simultanément avec une précision arbitraire. Il en est ainsi de la position et de l'impulsion qui obéissent à la relation :

,

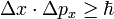
où x est la position de la particule selon un axe donné, p_x son impulsion le long de cet axe et Δx et Δp_x traduisent l'incertitude dans la mesure de la position et de l'impulsion respectivement.

Les expressions « incertitude » ou « incertitude de la mesure » peuvent être trompeuses. Elles pourraient laisser croire que cette incertitude n'est qu'une traduction de notre ignorance et de notre incapacité à effectuer une mesure sans perturber un objet aussi petit qu'une particule. Et donc que la particule a une position et une impulsion précise que nous ne connaissons pas. Cela est faux. L'étude de la mécanique quantique et de certains de ses paradoxes (voir Paradoxe EPR et Inégalités de Bell) montrent que cette incertitude est une propriété intrinsèque de la particule. On utilise d'ailleurs parfois l'expression de « principe d'indétermination » au lieu de « principe d'incertitude ». Disons plutôt que la particule a un état bien précis mais que sa traduction en concepts physiques classiques tels que position et impulsion n'est pas si simple.

Une telle relation existe aussi pour d'autres paires de variables comme la mesure du spin selon deux axes perpendiculaires ou pour l'énergie et le temps.

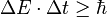
Mais que signifie une telle relation ? Car si la position d'une particule est quelque chose de parfaitement clair, le « temps » d'une particule l'est moins puisque celle-ci n'existe pas seulement en un seul instant !

Cette relation traduit plutôt la relation entre l'énergie d'un processus physique donné et sa durée.

Un exemple bien précis est donné par les raies d'émission des atomes lorsque les électrons changent de niveau d'énergie. Lorsqu'un électron est excité, il se retrouve sur une orbitale (un niveau) d'énergie plus élevée, puis, après un certain temps, il retombe spontanément dans un état d'énergie plus faible (éventuellement l'état de base) en émettant un photon d'énergie égale à la différence d'énergie de ces deux niveaux. Si l'électron reste longtemps sur le niveau excité (état métastable), alors la précision sur l'énergie sera grande et la fréquence du photon précise. Par contre, si le niveau excité est fortement instable, l'électron retombe très vite, la précision sur la durée est grande (Δt est au pire de l'ordre de la durée du processus) et l'incertitude sur l'énergie est grande. Cela se traduit par un élargissement des raies spectroscopiques.

Considérons maintenant le vide et un intervalle de temps t extrêmement court. Dans ce cas, l'incertitude sur l'énergie sera :

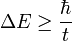
Si cette incertitude est suffisante, l'énergie peut être suffisante pour correspondre à une particule selon la relation E = mc². Il est donc possible que pendant un instant très bref on ait l'existence d'une particule. Cette particule apparaît "de rien", existe un bref instant, et disparaît presque aussi tôt.

C'est ce que l'on appelle les fluctuations du vide. Le vide serait remplit de particules virtuelles apparaissant et disparaissant en permanence. Elles seraient d'autant plus nombreuses que leur existence est courte.

L'énergie et l'impulsion ne sont pas les seules propriétés qui caractérisent les particules. Il existe d'autres propriétés qui doivent respecter des lois de conservation comme la charge électrique. Ainsi, pour les électrons, on ne peut avoir que l'apparition spontanée de paires électron - positron.

Une autre différence importante entre électrons et photons est leur masse propre. Les électrons ont une masse propre non nulle auquel correspond une énergie, selon E = mc², loin d'être négligeable. Ce n'est que pour des durées extrêmement courtes que de telles paires électron - positron peuvent exister, de l'ordre de . Par contre, des photons virtuels peuvent très bien avoir une durée de vie relativement grande pourvu que leur énergie (leur fréquence) soit très faible.

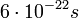
Ces étranges fluctuations du vide pourraient sembler être une vue de l'esprit. Une spéculation sur la relativité et le principe d'incertitude. D'autant que nous avons parlé de "particules non observées". Mais ce n'est pas le cas. Même sans les observer leur effet peut être mesurable. C'est le cas de l'effet Casimir.

Les calculs montrent que l'énergie du vide, résultant de ces fluctuations, est a priori infinie. Ce qui est logique puisqu'en prenant des durées arbitrairement courtes on a des énergies arbitrairement élevées. Par contre, la différence d'énergie entre deux situations données, par exemple selon la distance entre deux plaques conductrices comme dans l'effet Casimir, est finie et peut être calculée. Et le résultat est conforme aux observations.