Pseudo-potentiel - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - L'approche du pseudopotentiel - Méthode des ondes planes orthogonales - Pseudopotentiel empirique - Pseudopotentiel de Phillips-Kleinman-Antoncik - Pseudopotentiel à norme conservée

Méthode des ondes planes orthogonales

La méthode des ondes planes orthogonales (OPW pour orthogonalized planes waves) a été introduite par Convers Herring dans les années 1940. La méthode permit de mieux comprendre la nature de structure de bande de matériaux semiconducteurs tels que le silicium et le germanium et fut la première à expliquer de manière théorique que le silicium est un matériau à gap indirect. Le développement de cette méthode mérite d’être introduit car celle-ci est l’ancêtre direct de la notion de pseudopotentiel.

Formalisme mathématique

De manière concrète, la méthode OPW est une approche générale qui vise à construire des fonctions de bases pour la description des états de valence. Ces fonctions sont définies de la manière suivante :

$\chi^{OPW}_q(r)=\frac{1}{\Omega}[e^{iqr}- \sum_j <u_j|q>u_j(r)]$

Les fonctions uj sont arbitraires mais nécessitent d’être localisées autour des noyaux. De la définition précédente, il s’ensuite que chiqOPW est bien orthogonale à toutes les fonctions uj c’est-à-dire que pour tout uj :

$<u_j|\chi^{OPW}_q>=0$

Si les fonctions uj sont correctement choisies, l’expression (X) peut alors être vue comme étant la somme de deux contributions ; une partie adoucie (soft), c’est-à-dire ne comportant pas de nœuds, et une partie localisée. La partie adoucie peut être représenté aisément par une combinaison d’ondes planes ce qui était l’objectif d’Herring comme il le précise lui-même

« This suggest that it would be practical to try to approximate [the eigenfunction] by a linear combinaison of a few planes waves, plus a linear combinaison of a few function $u j$ localized about each nucleus and obeying wave equations of the form :

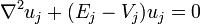
Le potentiel Vj et les fonctions uj qui apparaissent dans l’équation doivent être choisie de manière optimales. Il est important de préciser que, les états de valence étant étiquetés, par leurs nombres quantiques l et m, il est normal que les fonctions que l’on ajoute possèdent également les mêmes valeurs de l et m. Des précédentes définitions, les fonctions d’onde de valence peuvent être exprimées comme :

Pseudopotentiel empirique

Le concept de pseudopotentiel a été introduit dans les années 1930 par Fermi. Par la suite, Hellmann utilise cette notion pour le calcul des niveaux énergétiques de métaux alcalins. Ces premiers pseudopotentiels sont qualifiés d'empiriques; ce qui signifie qu'ils ne sont pas obtenus par calcul mais paramétrés pour reproduire au mieux des résultars expérimentaux de référence. L'utilisation d'un tel type de pseudopotentiel se fonde sur deux constatations. Tout d'abord, s'il était certain à cette époque que l'on pouvait obtenir de manière exacte et par calcul des pseudopotentiels cela passait par la résolution de calculs complexes (impliquant les fonction d'onde atomiques) impossible à résoudre sans ressources informatiques. L'utilisation d'une méthode empirique beaucoup plus simple allait donc de soi. Ensuite, on peut constater qu'un certain nombre d'éléments peuvent être décrit par des pseudopotentiels paramétrisés tout en fournissant une approximation acceptable de l'interaction électron de valence - ion de cœur. Cela était vrai notamment pour les métaux alcalins, les métaux "simples" tels que l'aluminium ainsi que les semi-conducteurs. L'utilisation de ces pseudopotentiels va permettrent en une dizaine d'année d'augmenter le champ des connaissances dans le domaine de l'état solide avant d'être remplacé par des pseudopotentiels ab initio plus efficaces.