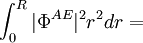Pseudo-potentiel - Définition
La liste des auteurs de cet article est disponible ici.
Pseudopotentiel de Phillips-Kleinman-Antoncik
C'est par une reformulation de la méthode OPW d'Herring qu'en 1959 Phillips et Kleinman développent la première approche formelle (non empirique) de la notion de pseudopotentiel. Antoncik, de manière indépendante, publie la même année une approche similaire. La méthode du pseudopotentiel de Phillips-Kleinman-Antoncik (PKA) est la première à montrer que la condition d'orthogonalité dans la région de cœur entre les états de cœur et de valence agit comme un potentiel répulsif qui tend à s'opposer au potentiel nucléaire attractif ressentit par les électrons de valence. Le plus souvent, ces deux effets se combinent pour former un potentiel faiblement répulsif, le pseudopotentiel.
Développement mathématique
Avantages et inconvénients
Pseudopotentiel à norme conservée
L'introduction du principe de pseudopotentiel à norme conservée représente la percée la plus significative dans le traitement des électrons de cœur. L'approche fut développée par Hamann, Schlüter et Chiang et fut suive peu de temps après par une méthode très similaire mais établie de manière indépendante par Kerker.
Méthodologie
La première étape dans la génération d'un pseudopotentiel à norme conservée consiste à réaliser un calcul atomique ab initio tous-électrons. La configuration électronique de l'atome peut être choisie arbitrairement. Généralement il s'agit de l'atome à l'état neutre. Le calcul se fait au départ de l'équation de Khon-Sham écrite sous sa forme radiale :
![[-\frac{1}{2}\frac{d^2}{dr^2}+\frac{l(l+1)}{2r^2}+\frac{-Z}{r}+V_H+V_{XC}]rR_{nl}(r)=\epsilon_{nl}rR_{nl}(r)](https://static.techno-science.net/illustration/Definitions/autres/2/20dc151ae8b7799fb3b81d4ab03215e3_4ef7147b1fd35fef9c8f4e900306e9ba.png)
La fonction d'onde réelle est ensuite remplacée par une pseudofonction d'onde à laquelle est associée un potentiel modèle (le pseudopotentiel) choisi pour reproduire correctement les propriétés des états de valence. Le schéma mathématique qui permet de générer la pseudofonction d'onde n'est pas unique. Il existe du point de vue mathématique une certaine liberté dans le choix de la méthode comme en témoignent les nombreuses publications qui présentent différentes manière de faire.
Conditions sur la pseudofonction
Pour obtenir un pseudopotentiel à norme conservée le plus efficace possible, la pseudofonction d'onde doit répondre à une liste de critère précis.
- Les énergies propres obtenus par un calcul tout électron et les pseudoénergies sont égales pour une configuration atomique de référence.
- Les pseudofonctions d’onde de valence et les fonctions d’onde de valence tout électron sont identiques au-delà d’un certain rayon de cœur rC choisi arbitrairement.
- L’intégration de 0 à rC pour chaque fonction d’onde est identique (condition de conservation de la norme)
- Les dérivées logarithmiques de la fonction d’onde tout électron et de la pseudofonction d’onde ainsi que leur dérivée première par rapport à l’énergie sont égales pour tout r ≥ rC.
Note: dans les formules suivantes, les notations AE et PS font référence respectivement aux résultats obtenus de manière ab initio et avec le pseudopotentiel.
Φ représente la fonction d'onde