Schéma produit - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie algébrique, le produit de deux schémas (plus exactement de deux schémas au-dessus d'un même schéma de base) est l'équivalent des produits d'anneaux, d'espaces vectoriels, d'espaces topologiques... C'est un outil de base pour construire des schémas, faire du changement de bases etc.
Définition
On fixe un schéma S (appelé schéma de base) et on considère la catégorie des S-schémas. Soient X,Y deux S-schémas. En langage catégoriel, le produit (fibré) de X,Y au-dessus de S est simplement le produit fibré de
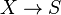
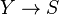
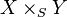
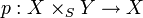
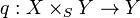
- pour tout S-schéma Z et pour tout couple de morphismes de S-schémas
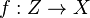
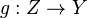
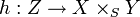
Proposition Le produit fibré
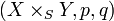
Comme toute solution d'un problème universelle, l'unicité découle immédiatement de la définition. L'existence se prouve en se ramenant au produit fibré de deux schémas affines au-dessus d'un schéma affine. On utilise alors le fait que le produit tensoriel de deux algèbres au-dessus d'un anneau commutatif unitaire A est la somme dans la catégorie des A-algèbres, catégorie opposée de la catégorie des A-schémas affines.
Notation On note généralement le produit fibré par
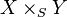
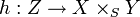
Exemples
- Si A,B sont des algèbres au-dessus d'un corps k. Alors
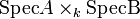
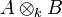
-
- Si
![A=k[T_1,\ldots, T_n]](https://static.techno-science.net/illustration/Definitions/autres/3/356402ebba225e01ca29ff486427c8b4_629f54ad6e9aaeac216a213e839b0937.png)
![B=k[S_1,\ldots, S_m]](https://static.techno-science.net/illustration/Definitions/autres/a/a92089a73e94f7b3b6cc3d890e87d5c0_cff82be8c266da72343cedc227088834.png)
![A\otimes_k B=k[T_1,\ldots, T_n, S_1, \ldots, S_m]](https://static.techno-science.net/illustration/Definitions/autres/a/a4c55d208e3a462333eb15fd2096caec_4f3c6c9e64cae40e70315ace3f00aad8.png)
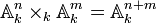
- Si
-
- Si
![A=k[T_1,\ldots, T_n]/I](https://static.techno-science.net/illustration/Definitions/autres/6/6ef4ccbfacce9925b3c31f59d47b4ece_f506a1ddcd3eda6f3514f402fb138b41.png)
![B=k[S_1,\ldots, S_m]/J](https://static.techno-science.net/illustration/Definitions/autres/8/8ea984ca5703030687e5986ee2b18796_be2a1224edac8b46d17f5d8488e19e59.png)
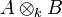
![k[T_1,\ldots, T_n, S_1, \ldots, S_m]](https://static.techno-science.net/illustration/Definitions/autres/8/83b6efce87baadb0fe6495432c160740_f0ddcaf8bbae3d3a51544a1592ab12fc.png)
- Si
- Le produit de la droite projective

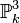
-
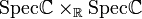

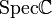
Premières propriétés
- Pour tout S-schéma Z, l'application
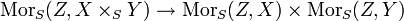
définie par
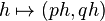
- Si X = SpecA,Y = SpecB et S = SpecR sont affines, alors
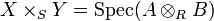
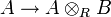
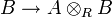
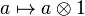
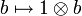
- Si U,V sont des parties ouvertes respectives de X,Y, alors
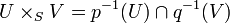
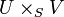
- On a des isomorphismes canoniques

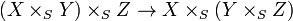
- Si Z est un Y-schéma, alors on a un isomorphisme canonique
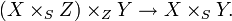
Changement de bases
Le concept du changement de bases est fondamental dans la théorie des schémas. Soit
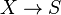
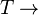
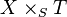
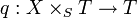
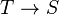
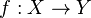
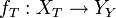
- Par exemple, si
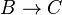
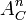
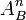

- Si K / k est une extension de corps,
![{\rm Spec} k[T_1, \ldots,T_n]/I](https://static.techno-science.net/illustration/Definitions/autres/9/982f18d9c53bef1320cedcb1d3135359_2182604d500bcd90e8e58be6b3696910.png)
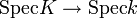
![{\rm Spec} (K[T_1, \ldots,T_n]/(I))](https://static.techno-science.net/illustration/Definitions/autres/1/173abcd48353fd7f375c769b87abc98e_c60ff4a28ecbddc3dd2d8b75c6225d07.png)
- Similairement,
![{\rm Proj} k[T_0, \ldots, T_n]/I](https://static.techno-science.net/illustration/Definitions/autres/2/2917031c104a1e164f87b8de962065d2_0334cc9ab68a33552e746e632a19f78f.png)
![{\rm Proj} (K[T_0, \ldots, T_n]/(I))](https://static.techno-science.net/illustration/Definitions/autres/8/81db500cce736496438c44a97d968fa2_38bb754f3541f40dd55aa2b0566c79bd.png)
Dans ces deux exemples, le changement de base est donné par une extension de corps. On parle alors d'extension du corps de base ou d'extensions des scalaires. Par exemple, une conique projective non-singulière devient isomorphisme à la droite projective après une extension quadratique séparable du corps de base.
- Si X est une variété algébrique sur un corps k et si K / k est une extension. Alors X(K) = XK(K) est l'ensemble des points rationnels de XK.

















































