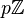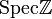Schéma produit - Définition
La liste des auteurs de cet article est disponible ici.
Espace topologique sous-jacent
Les points de
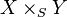
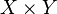
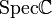

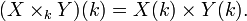
Donc on a un bon contrôle des points rationnels. Cependant, même quand k est algébriquement clos et que l'on se restrient aux points fermés (les points fermés de
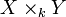
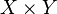
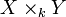
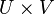
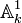
Fibres d'un morphisme
Soit
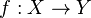
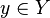
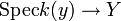
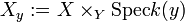
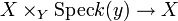
Si Y est irréductible de point générique η, la fibre Xη est appelée la fibre générique de f. Si y est un point fermé de Y, la fibre Xy est appelée une fibre fermée (ou la fibre spéciale lorsque Y est le spectre d'un anneau de valuation discrète).
Exemples
- Les fibres du morphisme structural de l'espace affine
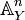
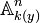
- Soit
![X={\rm Spec} (\Z[t, s]/(ts^2-p))](https://static.techno-science.net/illustration/Definitions/autres/a/a1cb2010cc9bfff4e3e76e07824fbef4_a4c79279f92f9339a7376717d859fd1a.png)
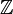
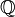
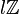
- Soit L / K une extension de corps de nombres et soient OK,OL leurs anneaux d'entiers respectifs. Soit
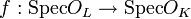
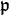
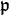
- Si E est une courbe elliptique sur
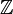
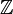
![{\rm Proj} \Z[X, Y, Z]/(Y^2Z+a_1XZY+a_3Z^2Y-(X^3+a_2X^2Z+a_4XZ^2+a_6Z^3)](https://static.techno-science.net/illustration/Definitions/autres/2/263f4b00d01e41b9e0317d68609f0d2c_3f54025e7ed614a4eb6ba2261d94accf.png)