Somme des angles d'un triangle - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie euclidienne, la somme des angles d'un triangle est égale à l'angle plat, soit 180 degrés ou π radians. Ce résultat est connu et démontré par Euclide, dans ses Éléments.
Il est équivalent à l'axiome des parallèles d'Euclide :
- Par un point donné, on peut mener une et une seule parallèle à une droite donnée.
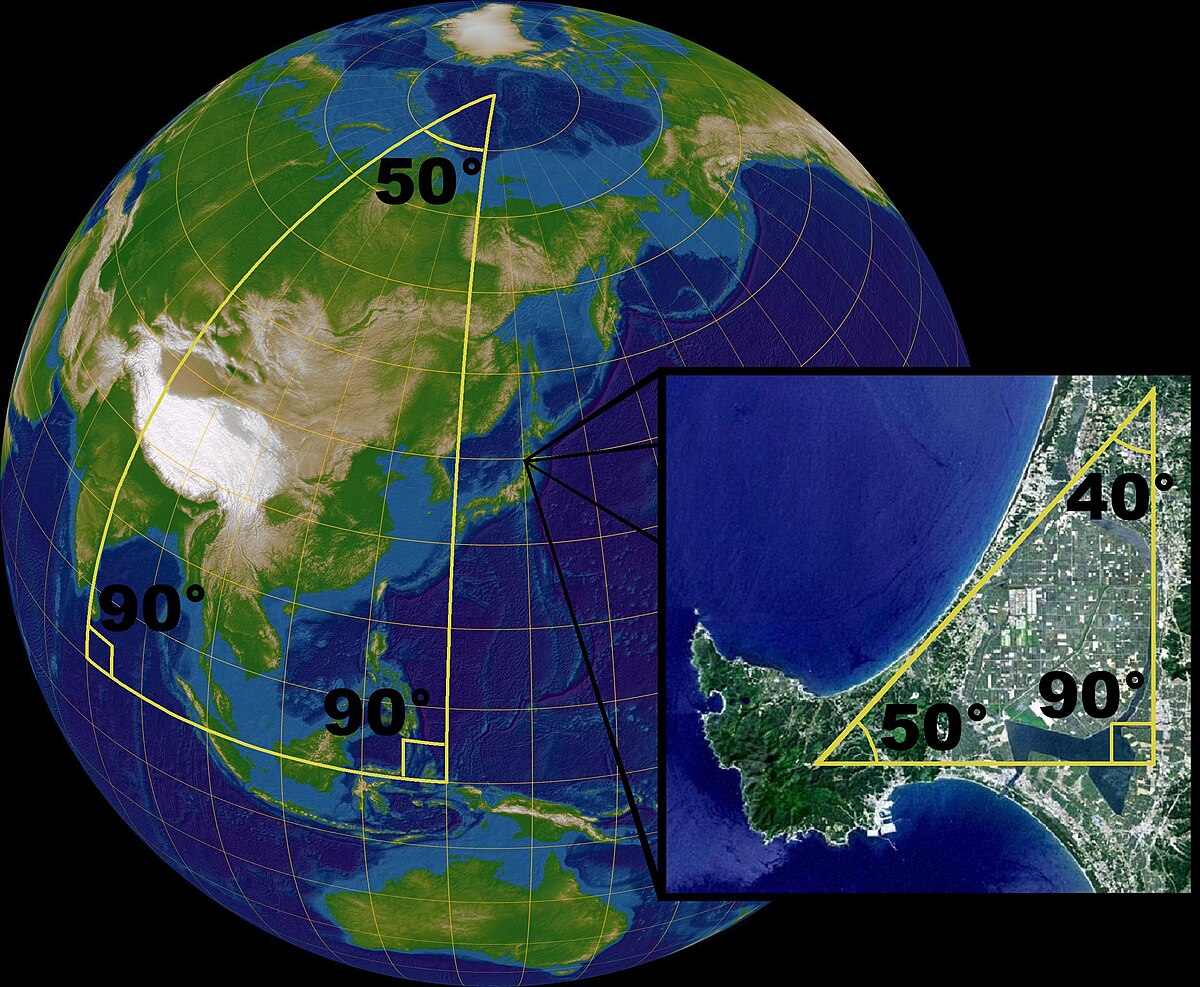
Mais il est possible de construire, tout aussi rigoureusement, d'autres géométries, dites non euclidiennes qui ne respectent pas cet axiome. La somme des angles d'un triangle n'est alors plus constante, mais elle permet de classifier ces géométries, la valeur de 180° gardant son importance : les géométries pour lesquelles la somme des angles d'un triangle est inférieure à 180° sont dites hyperboliques, celles pour lesquelles elle est supérieure à 180° sont elliptiques (comme par exemple la géométrie sphérique utilisée pour modéliser la géométrie à la surface de planètes comme la Terre).
En géométrie euclidienne
En géométrie euclidienne (la géométrie souvent considérée comme usuelle) la somme des angles de tout triangle est égale à 180°. Ainsi, la somme des angles est un invariant des triangles, qui permet de résoudre de nombreux problèmes élémentaires de résolution d'un triangle.
Théorème
Lorsqu'on parle de somme des angles d'un triangle, il est d'usage de considérer les mesures des angles géométriques, la proposition s'écrivant de façon plus rigoureuse (mais aussi plus lourde) :
Théorème — La somme des mesures des angles géométriques d'un triangle est égale à la mesure d'un angle plat.
Démonstration
La démonstration classique depuis Euclide repose sur le tracé de la droite parallèle à un côté du triangle et passant par le sommet qui n'appartient pas à ce côté. Ainsi, la propriété sur la somme des angles d'un triangle s'appuie sur l'axiome des parallèles. Différentes rédactions en ont été proposées au cours des siècles. Voici celle que donnait A. Amiot en 1870. Plutôt que de donner comme constante un angle plat, il parle, à la suite d'Euclide lui-même, de « deux angles droits ».
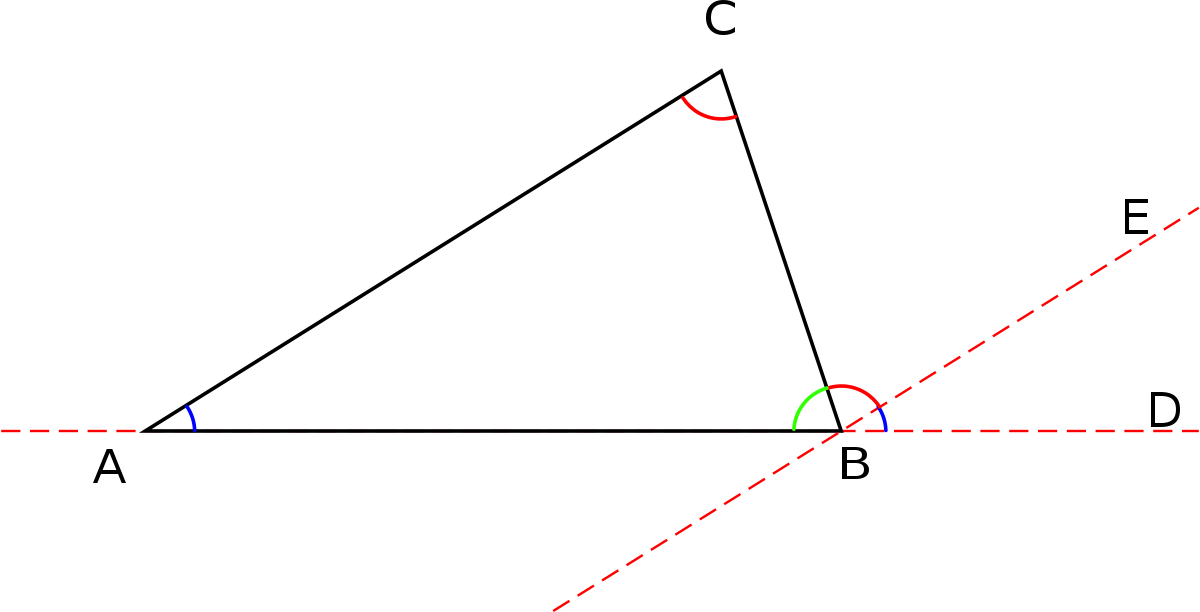
Démonstration classique, rédigée par A. Amiot — Soit le triangle ABC ; je prolonge le côté AB et je mène par le sommet B la ligne droite BE parallèle au côté opposé AC.
Les angles ACB, CBE sont égaux comme alternes-internes par rapport aux parallèles AC, BE et à la sécante BC ; les angles CAB, EBD sont aussi égaux comme correspondants par rapport aux mêmes parallèles et à la sécante AB. Donc, la somme des trois angles ABC, ACB, CAB du triangle est égale à la somme des trois angles adjacents ABC, CBE, EBD formés sur la ligne droite AD, c'est-à-dire qu'elle est égale à deux angles droits.
Trois points alignés
La démonstration précédente est valable pour un triangle vrai, défini par trois points non alignés. Mais la propriété est aussi vraie pour un triangle dégénéré constitué de trois points distincts alignés : si trois points A, B et C sont alignés dans cet ordre, les angles du triangle en A et C sont nuls et l'angle en B est plat.
Angles aigus et obtus
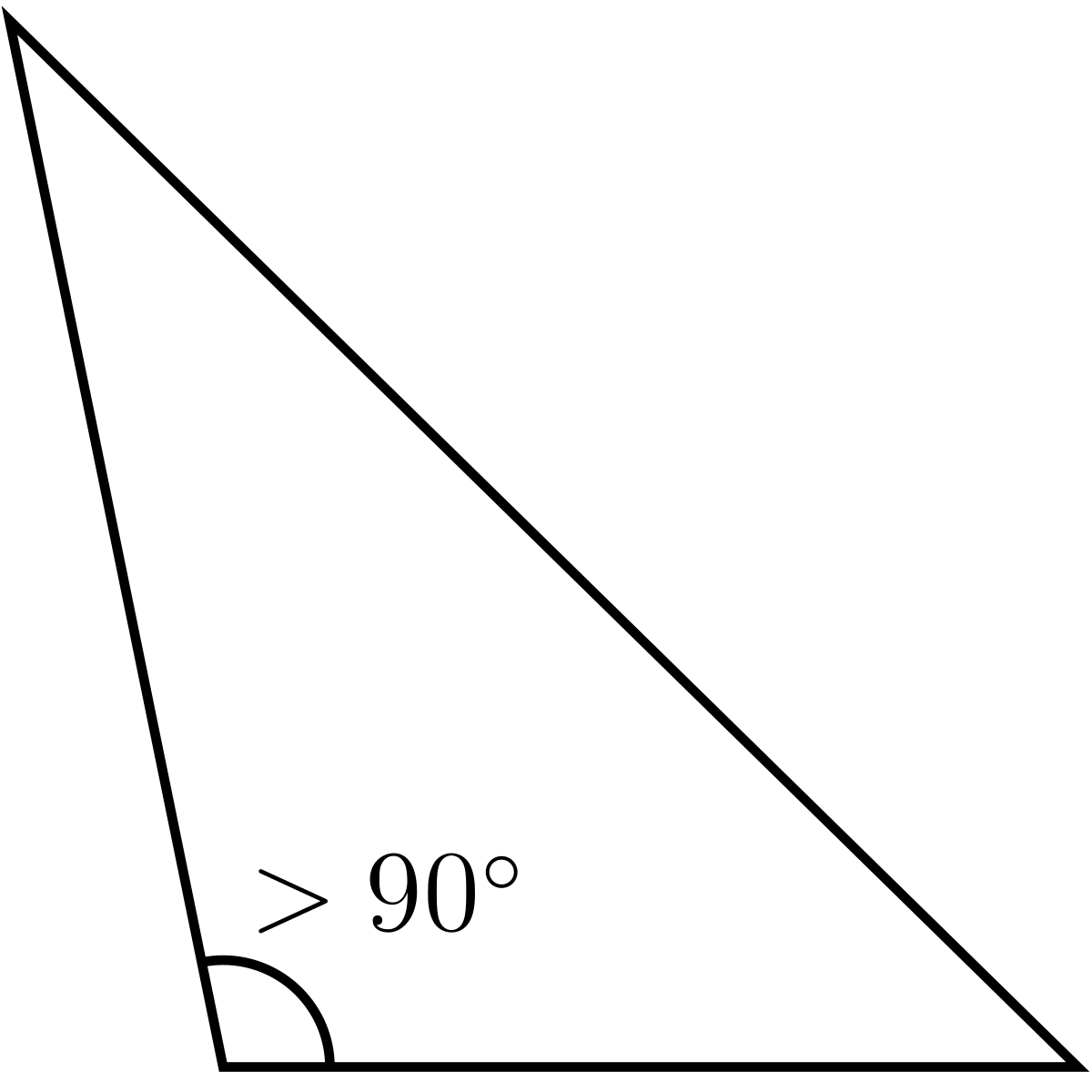
La mesure d'un angle géométrique étant un nombre positif, une première conséquence du théorème de la somme des angles est qu'un triangle ne peut posséder plus d'un angle obtus (c'est-à-dire un angle de mesure supérieure à 90°). En effet, si un triangle possédait deux angles obtus, la somme des mesures de ces deux angles et du troisième angle serait supérieure à 180.
Triangles particuliers
Un triangle équilatéral est un triangle dont les trois angles ont la même mesure. En notant a cette mesure et en utilisant la somme des angles d'un triangle, il vient :
- 3a = 180°
Donc les angles d'un triangle équilatéral mesurent 60° (ou encore π⁄3 radians).
Un triangle rectangle isocèle (demi-carré) possède un angle droit (de mesure égale à 90°) et deux angles égaux. En considérant que la somme des angles du triangle, il vient que les deux angles égaux sont aigus (de mesure inférieure à 90°), car sinon leur somme serait supérieure à 180. Donc leur somme est égale à 180 - 90 = 90°. Comme ils sont égaux, ces deux angles mesurent chacun 45°. Ainsi,
Triangle rectangle isocèle — Tout triangle rectangle isocèle possède trois angles de mesures respectives 90°, 45° et 45°.
Triangles semblables
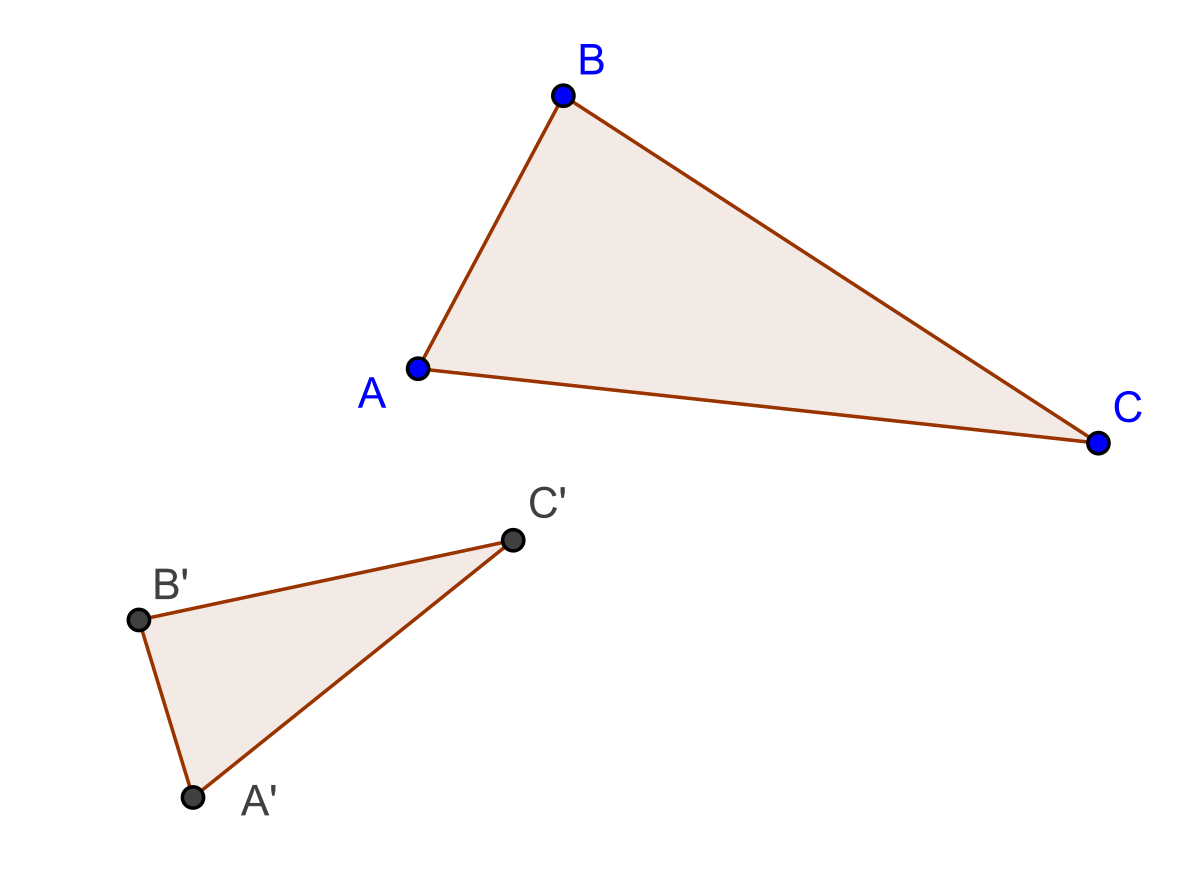
Deux triangles sont dits semblables lorsqu'ils ont « la même forme », c'est-à-dire lorsque chaque angle de l'un est égal à un angle de l'autre. Cette définition semble indiquer que, pour prouver que deux triangles sont semblables, il faut démontrer égalités. Or, en considérant la somme des angles du triangle, deux égalités suffisent : si deux angles a et b d'un premier triangle sont égaux à deux angles d'un autre, ces triangles sont semblables, car les troisièmes angles des deux triangles auront une mesure, en degrés, égale à 180 - (a + b). D'où la propriété :
Triangles semblables — Si deux angles d'un triangle sont égaux à deux angles d'un autre triangle, alors ces triangles sont semblables.
Conséquence pour les polygones
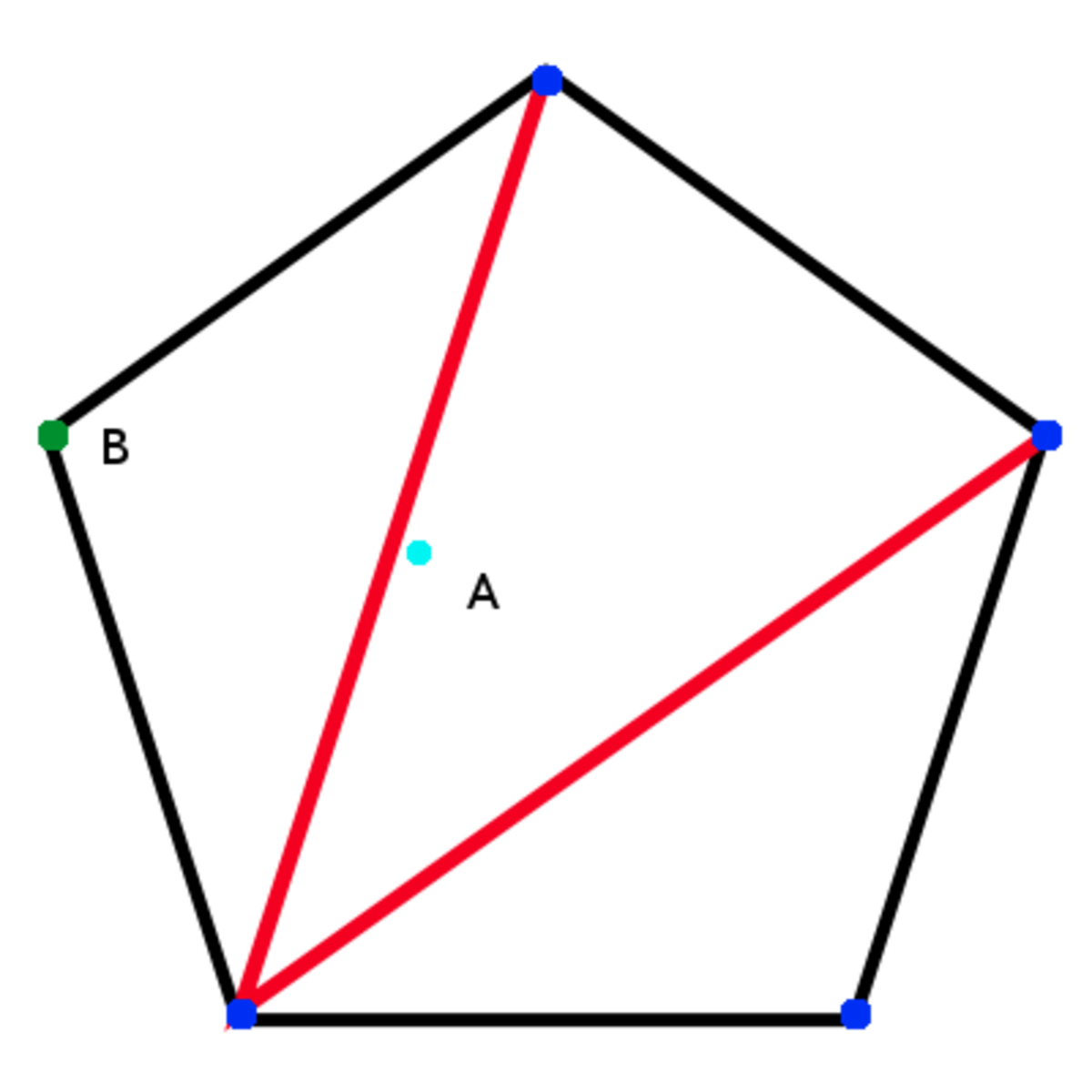
Tout polygone convexe (c'est-à-dire sans « creux ») à n côtés peut-être considéré comme constitué de n—2 triangles accolés deux à deux par un côté commun, qui est une diagonale de ce polygone. Pour cela, il suffit de considérer tous les segments joignant un certain sommet à tous les autres : il découpent le polygone en n—2 triangles ayant ce sommet en commun et dont la somme de tous les angles est égale à la somme des angles du polygone. Il est ainsi démontré que la somme des angles d'un polygone convexe à n côtés ne dépend pas de sa forme, c'est une constante égale à (n—2)×180°.