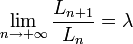Suite de Conway - Définition

Propriétés

Les principales propriétés de cette suite sont :

• Aucun terme de la suite ne comporte un chiffre supérieur à 3.
• Tous les termes de la suite possèdent un nombre pair de chiffres, sauf le terme initial.
• Les termes de rang impair se terminent par 11 et les termes de rang pair par 21 (là encore à l'exception du terme initial).
• En moyenne, les termes de la suite possèdent 50 % de chiffres 1, 31 % de 2 et 19 % de 3.
• Le nombre de chiffres du n^e terme de la suite est proportionnel à λⁿ, où est un nombre algébrique de degré 71 nommé constante de Conway. Plus précisément, si on note L_n le nombre de chiffre du n^e terme de la suite, alors :

  

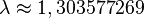
Cette propriété reste vraie dans le cas général où le premier terme de la suite est choisi différent de 1.

Racines du polynôme de Conway sur le plan complexe.

La constante de Conway est l'unique solution réelle positive de l'équation polynomiale suivante :

x⁷¹ − x⁶⁹ − 2x⁶⁸ − x⁶⁷ + 2x⁶⁶ + 2x⁶⁵ + x⁶⁴ − x⁶³ − x⁶² − x⁶¹ − x⁶⁰ − x⁵⁹ +

2x⁵⁸ + 5x⁵⁷ + 3x⁵⁶ − 2x⁵⁵ − 10x⁵⁴ − 3x⁵³ − 2x⁵² + 6x⁵¹ + 6x⁵⁰ + x⁴⁹ + 9x⁴⁸ − 3x⁴⁷ −

7x⁴⁶ − 8x⁴⁵ − 8x⁴⁴ + 10x⁴³ + 6x⁴² + 8x⁴¹ − 5x⁴⁰ − 12x³⁹ + 7x³⁸ − 7x³⁷ + 7x³⁶ + x³⁵ −

3x³⁴ + 10x³³ + x³² − 6x³¹ − 2x³⁰ − 10x²⁹ − 3x²⁸ + 2x²⁷ + 9x²⁶ − 3x²⁵ + 14x²⁴ − 8x²³ −

7x²¹ + 9x²⁰ + 3x¹⁹ − 4x¹⁸ − 10x¹⁷ − 7x¹⁶ + 12x¹⁵ + 7x¹⁴ + 2x¹³ − 12x¹² − 4x¹¹ −

2x¹⁰ + 5x⁹ + x⁷ − 7x⁶ + 7x⁵ − 4x⁴ + 12x³ − 6x² + 3x − 6 = 0

« Désintégration audioactive »

John Conway qualifia initialement cette suite de « désintégration audioactive » (audioactive decay en anglais), un jeu de mots sur la désintégration radioactive, en remarquant le comportement des différents termes de la suite.

Il montra qu'à partir d'un certain point, presque tous les termes de la suite peuvent être décomposés en 92 sous-termes (nommés éléments, par analogie avec les éléments chimiques) qui se décomposent au terme suivant en un certain nombre d'autres éléments.

Par exemple, l'élément le plus simple, nommé hydrogène, est la séquence 22 qui donne elle-même au terme suivant. La séquence 3113322112 est dénommée manganèse ; au terme suivant, elle donne 132123222112 qui se décompose en les séquences prométhium (132) et sodium (123222112).

Il a été montré que si l'on débute la suite par le terme uranium 3, les 91 autres éléments seront apparus dans un terme ou un autre au bout de 91 itérations. Cette suite porte d'ailleurs en anglais le terme de Conway's sequence.