Tenseur de Killing-Yano - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
sur les tenseurs
Tenseur
Tenseur (mathématiques)
Produit tensoriel
... de deux modules
... de deux applications linéaires
Algèbre tensorielle
Champ tensoriel
Espace tensoriel
Convention d'Einstein
Tenseur métrique
Tenseur énergie-impulsion
Tenseur de Riemann
... de Ricci
... d'Einstein
... de Weyl
... de Levi-Civita
... de Killing
... de Killing-Yano
... de Bel-Robinson
... de Cotton-York
Tenseur électromagnétique
Tenseur des contraintes
Tenseur des déformations
Modules
Algèbre extérieure
En géométrie riemannienne, un tenseur de Killing-Yano est une généralisation du concept de vecteur de Killing à un tenseur de dimension supérieure. Ils ont été introduits en 1952 par Kentarô Yano. Un tenseur antisymétrique d'ordre p
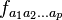
-
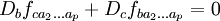
Cette équation diffère de la généralisation usuelle du concept de vecteur de Killing à des tenseurs d'ordre plus élevé, appelés tenseurs de Killing par ce que la dérivée covariante D est symétrisée avec un seul indice du tenseur et non la totalité de ceux-ci, comme c'est le cas pour les tenseurs de Killing.
Tenseurs de Killing-Yano triviaux
Tout vecteur de Killing est un tenseur de Killing d'ordre 1 et un tenseur de Killing-Yano.
Le tenseur complètement antisymétrique (dit de Levi-Civita)
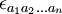
Propriétés
Un certain nombre de propriétés des espaces-temps quadridimensionnels impliquant les tenseurs de Killing-Yano ont été exhibées par C. D. Collinson et H. Stephani dans le courant des années 1970.
- Si un espace-temps admet un tenseur de Killing-Yano non dégénéré, alors celui-ci peut s'écrire sous la forme
-
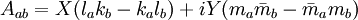
- où k, l, m et
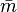
-
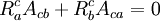
- Les solutions aux équations d'Einstein dans le vide et de type D dans la classification de Petrov admettent un tenseur de Killing et un tenseur de Killing-Yano, tous deux d'ordre 2 et reliés par la formule donnée ci-dessus.
- Si un espace-temps admet un tenseur de Killing-Yano d'ordre 2 dégénéré Aab, alors celui-ci s'écrit sous la forme
- Aab = kapb − pakb,
- k étant un vecteur de Killing de genre lumière. Le tenseur de Weyl est dans ce cas de type N dans la classification de Petrov, et k est son vecteur propre non trivial. De plus, a possède la relation donnée ci-dessus avec le tenseur de Riemann
- Si un espace-temps admet un tenseur de Killing-Yano d'ordre 3, alors soit le vecteur associé par dualité de Hodge est un vecteur de genre lumière constant, soit l'espace est conformément plat.
Construction de tenseurs de Killing à partir de tenseurs de Killing-Yano
Il existe plusieurs façons de construire des tenseurs de Killing (symétriques) à partir de tenseurs de Killing-Yano.
Tout d'abord, deux tenseurs de Killing triviaux peuvent être obtenus à partir de tenseurs de Killing-Yano :
- À partir d'un tenseur de Killing-Yano d'ordre 1 ξa, on peut construire un tenseur de Killing Kab d'ordre de 2 selon
- Kab = ξaξb.
- À partir du tenseur complètement antisymétrique
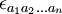
-
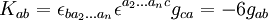
De façon plus intéressante, à partir de deux tenseurs de Killing-Yano d'ordre 2 Aab et Bab, on peut construire le tenseur de Killing d'ordre 2 Kab selon
-
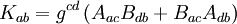
À partir d'un tenseur de Killing-Yano d'ordre n-1,
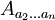
-
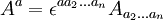
Du fait que le tenseur
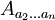
-
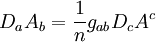
Cette propriété permet de construit un tenseur de Killing Kab à partir de deux tels vecteurs, défini par :
- Kab = AaBb + AbBa − 2AcBcgab.
Toute combinaison linéraire de tenseurs de Killing-Yano est également un tenseur de Killing-Yano.

















































