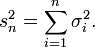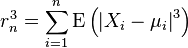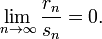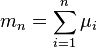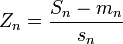Théorème central limite - Définition

Intérêt de ce théorème

On peut parfois lire dans la presse générale que la courbe en cloche représente la loi du hasard, ce qui n'a pas grande signification. Le succès sans égal de la loi de Gauss est la conséquence directe du théorème de la limite centrale et il est renforcé par la commodité relative d'utilisation de cette loi.

En elle-même, la convergence vers la loi normale de nombreuses sommes de variables aléatoires lorsque leur nombre tend vers l'infini n'intéresse que le mathématicien. Pour le praticien, il est intéressant de s'arrêter un peu avant la limite : la somme d'un grand nombre de ces variables est presque gaussienne, ce qui fournit une approximation souvent plus facilement utilisable que la loi exacte.

En s'éloignant encore plus de la théorie, on peut dire que bon nombre de phénomènes naturels sont dus à la superposition de causes nombreuses, plus ou moins indépendantes. Il en résulte que la loi normale les représente de manière raisonnablement efficace.

À l'inverse, on peut dire qu'aucun phénomène concret n'est vraiment gaussien car il ne peut dépasser certaines limites, en particulier s'il est à valeurs positives.

Généralisations du théorème central limite

Condition de Lyapounov

Soit X_n une séquence de variables définies sur le même espace de probabilité. Supposons que X_n ait une espérance finie μ_n et un écart-type fini σ_n. Nous définirons

Supposons que les moments centrés d'ordre 3

soient finis pour tout n et que

(C'est la condition de Lyapounov ).

Considérons de nouveau la somme . L'espérance mathématique de S_n est

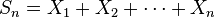
et son écart-type s_n. Si nous normalisons S_n en posant

alors la loi de Z_n converge vers la loi normale centrée réduite N(0,1) comme ci-dessus.

Condition de Lindeberg

Avec les mêmes définitions et les mêmes notations que précédemment, nous pouvons remplacer la condition de Lyapounov par la suivante qui est plus faible (Lindeberg 1920). Pour tout ε > 0

où E( U : V > c ) représente l'espérance conditionnelle : l'espérance de U sous la condition V > c. Alors la loi de Z_n converge vers la loi normale centrée réduite N(0,1).

Cas des variables dépendantes

Il existe quelques théorèmes qui traitent le cas de sommes de variables dépendantes, par exemple le théorème central limite pour les suites m-dépendantes, le théorème central limite pour les martingales et le théorème central limite pour les processus mélangeants.