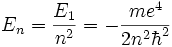Théorie de Pauli de l'atome d'hydrogène - Définition

Résultat final

Au final, on trouve une énergie E(l,m,k) indépendante de m, soit E(l,k), mais, de façon incroyable (sauf pour Pauli), ne dépendant que de la somme l+k-1 = n , qui doit être un entier positif, et appelé nombre quantique principal.

C'est la fameuse équation déjà trouvée par Bohr en 1913:

Il y a ce qu'on appelait une dégénérescence accidentelle, avant l'introduction par Pauli en mécanique quantique du vecteur de Runge-Lenz.

La multiplicité, g, du niveau d'énergie En est donc :

pour l variant de 0 à n-1 et

pour m variant de -l à +l

.

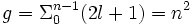
Et, compte-tenu du spin (1/2) de l'électron ,g vaut le double , soit 2.n²

• Donc couche K, g=2 ; L, g=8 ; M, g=18 ; O, g= 32 ; P, g = 50 ; Q, g=72 ; R, g = 98 ; S, g= 128.

Inutile d'aller plus loin pour décrire la classification périodique, la configuration de l'élément Z= 119 est celle d'un alcalin :

(1s²)(2s²)(2p^6)(3s²)(3p^6)(4s²)(3d^10)(4p^6) soit Kr(Z=36) puis,

(5s²)(4d^10)(5p^6) (6s²)(4f^14)(5d^10)(6p^6) Rn(Z=86) , puis

(7s²)(5f^14)(6d^10)(7p^6) Uuo(Z=118),

puis 8s.

Sur les 64 orbitales de la couche S, n= 8 , on n'a besoin de connaître seulement l'orbitale (8s): ce calcul requiert la mécanique quantique relativiste , car les électrons (1s²) de la première couche sont soumis à cette mécanique, impérativement.

De même, la configuration de l'élément Z= 121 est Uuo,(8s²,5g), la sous-couche 5g pouvant contenir jusqu'à 2*9 =18 électrons.

- -

Ce faisant, on obtiendra ainsi tous les niveaux d'énergie des éléments et des séries isoélectroniques, ce qui permettra de décrire certains traits de la classification périodique.

• Pour revenir à l'atome d'hydrogène, il ne reste plus qu'à introduire le vecteur de Runge-Lenz quantique pour comprendre que la dégénérescence dite "accidentelle" ne l'est pas : il y a bien une symétrie de plus que la simple symétrie centrale dans le cas de ce modèle de Rutherford quantique (cf théorème de Bertrand).

Auparavant, on va finir le raisonnement de Schrodinger(1926); puis on reviendra sur celui, plus subtil, de Pauli (1925).

Équation radiale-réduite

Si l'on revient à l'équation radiale de Leibniz-Schrodinger, on peut démontrer que pour r voisin de zéro, S(r) varie comme r^(l+1) , et que pour r très grand, S" + 2E S = 0 . Il est courant de poser 2E = -1/n² et donc S(r) varie comme exp (- r/n) à l'infini : n pour l'instant n'est qu'un réel!

Alors le dernier changement de fonction inconnue est logiquement l'essai suivant qui se révèle fructueux : S(r) = r^(l+1).exp(-r/n).g(r) ; mais on s'aperçoit qu'en changeant la variable r en s : = 2r/n l'équation s'arrange mieux :

L'équation radiale-réduite devient :

s f"(s) + (2l+2-s) f'(s) + (n-l-1) f(s) = 0 , avec g(r) = f(2r/n) = f(s)

Les matheux et Schrodinger ont reconnu cette équation immédiatement ( ?) : elle conduit à la fonction hypergéométrique dégénérée de Kummer, qui conduit aux polynômes de Laguerre, ssi n-l-1 est un entier positif : donc n est un entier positif et l = 0, 1 , 2 , .. ,n-1 . Et le nombre k est simplement k = n+l-1.

• Pour le cas l= n-1 (les états de Rydberg (cf. atome de Rydberg), elle devient r .g " + (2n-r) g' = 0 satisfaite par g = cste (en effet S(r) ne doit avoir aucun nœud quand le nombre quantique radial k est nul !).
• Ici, on fera les calculs "à la main" pour les faibles valeurs de n .Mais sinon, les afficionados des équations différentielles chercheront un développement de f(s) en série entière qui se STOPPE en un polynôme P(s): cela marche, c'est le raisonnement typiquement utilisé avec l'équation hypergéométrique !