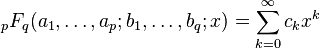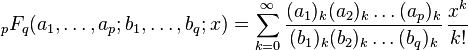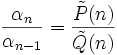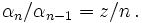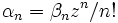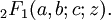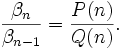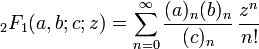Série hypergéométrique - Définition
En mathématiques, une série hypergéométrique est la somme d'une suite de termes tels que le quotient du terme d'indice k+1 par le terme d'indice k est une fonction rationnelle de k.
La série, lorsqu'elle converge, définit une fonction hypergéométrique qui peut ensuite être étendue à un domaine plus grand par prolongement analytique. On écrit généralement la série hypergéométrique comme suit :
où c0=1 et
-
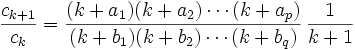
On peut aussi l'écrire :
où
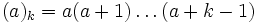
Introduction
Une serie hypergéométrique est une série formelle dans laquelle le quotient des coefficients successifs
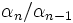
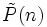
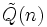
Ainsi, par exemple, dans le cas d'une série géométrique, ce quotient est une constante. Un autre exemple est la serie de Taylor de la fonction exponentielle où
En pratique, la série est écrite comme une série génératrice exponentielle, en modifiant les coefficients pour que le terme général de la série soit de la forme
et β0 = 1. Ici la variable z correspond à une constante dans le quotient
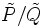
De nombreuses suites intéressantes en mathématiques ont la propriété que le quotient de deux termes successifs est une fraction rationnelle. Cependant, lorsqu'on les encode dans une série génératrice exponentielle, celle-ci a un rayon de convergence non nul seulement sous certaines conditions. Par convention, le terme de série hypergéométrique est d'ordinaire réservé au cas où la série definit une vraie fonction analytique avec un rayon de convergence strictement positif. Une telle fonction et son prolongement analytique éventuel est appelée une fonction hypergéométrique.
Des conditions de convergence ont été données par Carl Friedrich Gauss, dans le cas de
-
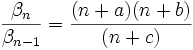
qui correspond à la série hypergéométrique standard classique
Notation
La notation standard pour la série hypergéométrique générale est
-
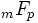
où les entiers m et p sont les degrés des polynômes P et Q dans le quotient
Si m>p+1, le rayon de convergence est nul et il n'y a pas de fonction analytique associée. La série se termine au bout d'un nombre fini de termes si jamais P(n) s'annule en un entier naturel n. Si Q(n) est nul, les termes de la suite ne sont pas définis.
La notation complète pour F suppose que P et Q sont unitaires et factorisés, de telle sorte qu'elle comprend un m-uplet qui est la liste des zéros de P et un p-uplet pour ceux de Q. Par le théorême fondamental de l'algèbre, ceci n'est pas vraiment une restriction. Par ailleurs, on peut aussi absorber les coefficients dominants de P ou Q en changeant z. Sous cette forme, le terme général de la suite est un produit de quotients de symboles de Pochhammer. Comme la notation de Pochhammer pour les factorielles ascendantes est traditionnelle, il est plus commode d'indexer F par les listes des opposés des zéros de P et Q. Ainsi, on a
où
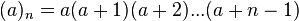
Cas particuliers et applications
Les polynômes orthogonaux classiques s'expriment tous comme des cas particuliers de 2F1 avec au moins un des parametres a et b entier negatif. De même, les fonctions de Legendre sont aussi des cas particuliers.
Les applications des séries hypergéométriques comprennent aussi l'inversion des intégrales elliptiques.
La fonction de Kummer 1F1(a,b;x) est une fonction hypergéométrique confluente.
La fonction 2F1 a plusieurs representations intégrales, dont l'intégrale hypergéométrique d'Euler.
Histoire et généralisations
Les travaux du XIXe siècle comprennent ceux de Ernst Kummer et la caractérisation fondamentale par Bernhard Riemann de la fonction F par le biais de l'équation différentielle qu'elle vérifie. Riemann a demontré que l'équation différentielle du second ordre (en la variable z) pour F, considérée dans le plan complexe, pouvait être caractérisée (sur la sphère de Riemann) par ses trois singularités régulières : que toute la partie algorithmique de la théorie était une conséquence de résultats de base et de l'usage des transformations de Möbius comme groupe de symétrie.
Par la suite, les series hypergéométriques ont été généralisées au cas de plusieurs variables complexes, par exemple par Paul Appell, mais une théorie générale comparable a mis du temps à apparaître. De nombreuses identités ont été découvertes, dont quelques unes remarquables. Des analogues avec un paramètre q ont été trouvées. Durant le XXe siècle, les fonctions hypergéométriques ont formé une partie active des mathématiques combinatoires, avec de nombreuses interactions avec les autres domaines. Il y a plusieurs définitions nouvelles de généralisations des fonctions hypergéométriques, notamment par Aomoto et Gel'fand. Il y a des applications à la combinatoire des arrangements d'hyperplans.
On peut définir des séries hypergéométriques sur des espaces symétriques riemanniens et sur des groupes de Lie semi-simples. Leur importance transparait dans l'exemple suivant : la serie hypergéométrique 2F1 est très proche des polynômes de Legendre et exprime, vue comme harmonique sphérique, les propriétés de symétrie de la sphère de Riemann.