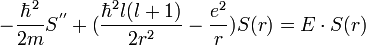Théorie de Pauli de l'atome d'hydrogène - Définition

Introduction

Cet article suit l'article atome d'hydrogène.

La résolution de l'équation de Schrödinger, écrite en coordonnées polaires, se découple des variables (θ,φ) et conduit à une équation à une dimension en r, appelée équation radiale de Leibniz-Schrödinger, puisque ce n'est jamais que la célèbre équation de Leibniz de 1685 traduite en mécanique quantique.

Mais l'équation de Schrödinger (1926) peut se résoudre autrement comme Pauli l'a montré en 1925 !

Équation radiale

L'équation radiale 1D de Leibniz-Schrödinger s'écrit pour r>0:

avec E valeur propre négative ,

et S(r) s'annulant "vite" à l'infini, et S(0) =0 :il s'agit donc d'un problème aux limites dit de Sturm (par opposition à un problème aux conditions initiales, dit de Cauchy).

[On reconnaît dans la barrière centrifuge de Leibniz ( l entier positif) (l=0 correspond à L =0 ; le problème classique n'a pas de correspondant simple en mécanique quantique, encore que ... )].

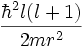
• Comment arrive-t-on à cette équation radiale de Leibniz-Schrodinger ?

Il SUFFIT de chercher la fonction d'onde Ψ(x,y,z,t) en coordonnées sphériques sous la forme :

• ,

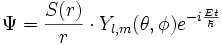
où les Y(l,m) sont les fonctions harmoniques sphériques. On appelle ce procédé courant dans les équations aux dérivées partielles, la séparation des variables. Souvent, on appelle R(r) := S(r)/r , la partie radiale de la fonction d'onde.

• Note importante annexe :

Harmoniques sphériques

Il n'y a rien de mystérieux (et surtout rien à voir avec la MÉCANIQUE quantique) dans ce qui semble être un tour de passe-passe. L'étude en électrostatique classique de l'opérateur Laplacien conduit à ces mêmes fonction Y(l,m) , appelées harmoniques sphériques, qui sont des fonctions usuelles dès que la symétrie sphérique entre en jeu. L'entier relatif m ne peut prendre que 2l+1 valeurs, de m = -l à m = +l , l étant un entier positif.

Ce sont ces harmoniques sphériques qui "quantifient" le problème sphérique par les deux nombres quantiques l et m (comme il est usuel dans tout problème de Sturm, dit "aux limites", des équations différentielles), ces deux entiers l et m qui auront tant d'importance dans l'étude de l'atome à N électrons et donc de la Classification périodique.

• Pour ne pas encombrer l'article Harmonique sphérique, est expliqué ici juste le minimum pour comprendre comment elles interviennent à ce niveau modeste (l=0,1,2,3):les (2l+1)polynômes r^lY_l,m forment une base sur l'ensemble des polynômes homogènes P(x,y,z) de degré l, harmoniques( c’est-à-dire dont le laplacien est nul)
• l=0 :  : c'est bien un polynôme de degré zéro, normé sur la sphère unité puisque son carré vaut 1/4Pi.

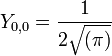
Dorénavant, nous n'indiquerons plus ce facteur dit de normalisation.

• l=1 :3 fonctions

 ;

;

;

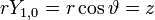
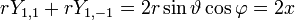
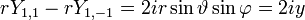
soit la base {x,y,z} dite orbitales p_x, p_y, p_z

• l=2: cinq fonctions

 ;

; et avec moins , 2i yz ;

;

;

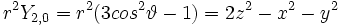
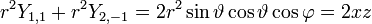
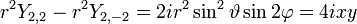
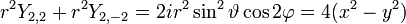
Soit la base dont chaque fonction est de laplacien nul.

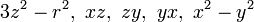
• l=3: 7 fonctions

soit la base dont chaque fonction est de laplacien nul.

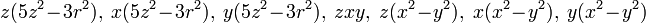
• l quelconque : on trouve une base de (2l+1) polynômes réels, mais bien sûr toute combinaison linéaire complexe reste dans ce sous-espace vectoriel sur le corps des complexes.Pourquoi (2l+1)? la raison en est aisée : il y a (l+1)(l+2)/2 polynômes homogènes de 3 variables (c'est le nombre de manières d'avoir avec un triplet d'entiers{m,n,p]la relation m+n+p = l). Quand on calcule le laplacien on tombe sur l'espace des polynômes homogènes de degré (l-2),de dimension (l-1)l/2 ,pour l >1 ce qui donne pour l'annulation du Laplacien autant de conditions. Donc il ne reste, pour les polynômes homogènes harmoniques qu'un sous-ev de dimension (l²+3l+2 -l²+l)/2 = 2l+1.

• Théorème: est fonction propre du laplacien avec la valeur propre -l(l+1):

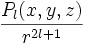
C'est ce théorème qui est sans arrêt utilisé pour la théorie de l'atome d'hydrogène.

En chimie ,on représente souvent les fonctions 1/r^(2l+1) . Pl comme les harmoniques sphériques des oribtales l ; parfois on prend leur carré; etc.

Ce sont les seules fonctions qui interviennent dans l'atome à N électrons pour N< 119 : donc cela suffit au physicien de l'atome, qui leur a donné des noms et des représentations mnémotechniques diverses. Ne pas oublier que l'on peut combiner à volonté ces fonctions, pour former ce que les chimistes appellent des orbitales hybridées du sous espace propre du niveau d'énergie En.