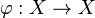Théorie ergodique - Définition

Définition de l'ergodicité

L'application est dite ergodique pour une mesure donnée si et seulement si tout ensemble mesurable invariant sous est de mesure nulle, ou de complémentaire de mesure nulle.

L'ergodicité capture la notion d'irréductibilité en théorie de la mesure : pour toute partition d'un système dynamique ergodique en deux sous-systèmes invariants, l'un des deux est trivial ou négligeable, au sens où il vit sur un ensemble de mesure nulle.

Une application satisfaisant cette propriété était autrefois également dite « métriquement transitive ».

Exemple : le flot ergodique sur une variété

• L'ergodicité du flot géodésique sur une variété à courbure négative a été découverte par Hopf en 1939.

• La relation entre le flot géodésique et les sous-groupes à un paramètre de SL2(R) a été établie par Fomin et Gelfand en 1952.

• L'ergodicité du flot géodésique sur les espaces symétriques a été établie par Mautner en 1957.

• Un critère simple pour l'ergodicité d'un flot homogène sur un espace homogène d'un groupe de Lie semi-simple a été établi par Moore en 1966.

• Beaucoup des théorèmes et résultats de ce domaine d'étude sont typiques de la théorie de la rigidité

• Les flots d'Anosov constituent un exemple de flots ergodiques sur SL2(R) et, plus généralement, sur une surface de Riemann à courbure négative. La plupart des développements à ce sujet se généralisent à des variétés hyperboliques à courbure négative constante, celles-ci pouvant être vues comme l'espace quotient d'un espace hyperbolique simplement connexe par un groupe discret de SO(n,1).

Hiérarchie ergodique

Système mélangeant

On dit que le système est mélangeant si quels que soient les événements (ensembles) A et B dans , la corrélation

tend vers 0 lorsque n tend vers l'infini.

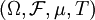
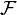
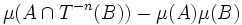
Hyperbolicité et système d'Anosov

Système de Bernoulli

La hiérarchie ergodique

Problèmes ouverts

Le mathématicien Sergiy Kolyada maintient une liste de problèmes ouverts en théorie ergodique sur son site web.

Théorie ergodique & mécanique statistique

En dépit de progrès importants réalisés en théorie ergodique depuis la formulation par Boltzmann de l'hypothèse ergodique, son utilisation pour justifier l'utilisation de l'ensemble microcanonique en mécanique statistique reste à ce jour controversée.

Bibliographie

Aspects historiques

• M. Mathieu ; On the origin of the notion "Ergodic Theory", Expositiones Mathematicae 6 (1988) 373.

• Giovanni Gallavotti ; Ergodicity, ensembles, irreversibility in Boltzmann and beyond, (1994). Texte complet disponible sur l'ArXiv : chao-dyn/9403004.

Ouvrages modernes

• Vladimir I. Arnold & André Avez ; Ergodic Problems of Classical Mechanics, Advanced Book Classics, Pearson Addison Wesley (Mai 1989), ASIN 0201094061.

• Ya G. Sinaï ; Introduction to Ergodic Theory, Princeton University Press (1976), ISBN

• I.P. Cornfeld, S.V. Fomin & Y.G. Sinai ; Ergodic Theory, # Springer-Verlag (1982), ISBN 3-540-90580-4.

• Karl Petersen ; Ergodic Theory, Cambridge Studies in Advanced Mathematics, Cambrides University Press (1983), ISBN 0-521-38997-6.

• Yakov Pesin & Luis Barreira ; Lyapunov Exponents and Smooth Ergodic Theory, University Lecture Series 23, American Mathematical Society, Providence (2001), ISBN 0-8218-2921-1.

• Tim Bedford, Michael Keane & Caroline Series (eds.) ; Ergodic theory, symbolic dynamics and hyperbolic spaces, Oxford University Press (1991), ISBN 0-19-853390-X.

• Jean Moulin Ollagnier ; Ergodic Theory and Statistical Mechanics, Lecture Notes in Mathematics 1115, Springer-Verlag (1985).

• Henk van Beijeren ; On some common misconceptions regarding the "Ergodic Hierarchy", (2004). Texte complet disponible sur l'ArXiv : cond-mat/0407730.

Articles originaux

• Eberhard Hopf ; Ergodic theory & the geodesic flow on a surface of constant negative curvature, Bulletin of the American Mathematical Society 77(6) (1971) 863.

• Eberhard Hopf ; Differential geometry in the large - 1956 lectures notes, Lectures Notes in Mathematics 1000, Springer-Verlag (1983).

• G.A. Margulis ; Application of ergodic theory to the investigation of manifold of negative curvature, Functionnal Analysis & Applications 3 (1969) 355.

• Y. Pesin ; Characteristic Lyapounov exponents & smooth ergodic theory, Russian Mathematical Surveys 32(4) (1982) 54.

• Y. Pesin ; Geodesic flows with hyperbolic behaviour of the trajectories & objects connected with them, Russian Mathematical Surveys 36 (1981) 1.

Bibliothèque virtuelle

• Joël Lebowitz & Oliver Penrose ; Modern Ergodic Theory, Physics Today, 26 (February 1973), 155-175. pdf.

• David Ruelle ; Ergodic theory of differentiable dynamical systems, Publications Mathématiques de l'IHÉS 50 (1979), 27-58. Texte complet disponible au format pdf.

• Mark Pollicott ; Lectures on ergodic theory, geodesic flows and related topics, Ulm (2003). Notes de cours non corrigées au format pdf.

• Charles Pugh & Michael Shub (appendix by Alexander Starkov) ; Stable ergodicity, Bulletin of the American Mathematical Society 41 (2004), 1-41. Texte disponible en ligne.