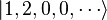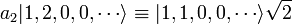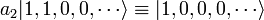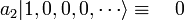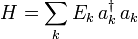Théorie quantique des champs - Définition
La liste des auteurs de cet article est disponible ici.
Champs quantiques
Notion de champ quantique
La façon dont la théorie des champs fut introduite par Dirac à partir des particules élémentaires est connue pour des raisons historiques sous l'appellation de seconde quantification.
- Les champs ne sont pas liés à la dualité onde-corpuscule.
Les particules élémentaires possèdent déjà cette dualité dans l'acceptation du terme de la mécanique classique. Ce que l'on entend par champ est un concept qui permet la création ou l'annihilation de particules en tout point de l'espace. Comme tout système quantique, un champ quantique a un hamiltonien et obéit à l'équation de Schrödinger :
(En théorie des champs, le formalisme lagrangien est plus facile à utiliser que son équivalent hamiltonien.)
- Avec la seconde quantification, l'indiscernabilité des particules s'exprime en termes de nombre d'occupation.
Supposons que N = 3, avec une particule dans l'état φ1 et deux dans l'état φ2, alors la fonction d'onde est :
alors qu'avec la seconde quantification, cette fonction est simplement
Quoique la différence soit minime, la deuxième permet d'exprimer facilement des opérateurs création et annihilation, qui ajoutent ou enlèvent des particules à l'état. Ces opérateurs sont très similaires à ceux définis par un oscillateur harmonique quantique qui, en mécanique quantique, crée ou détruit des quanta d'énergie.
Par exemple, l'opérateur a2 a l'effet suivant:
(Le facteur

Enfin, il faut introduire « les opérateurs de champ » de création ou d'annihilation d'une particule en un point de l'espace.
De même que pour une seule particule la fonction d'onde s'exprime avec son moment cinétique, de même les opérateurs de champ peuvent s'exprimer à l'aide des transformées de Fourier.
Par exemple,
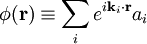
Les hamiltoniens, en physique des particules, sont écrits comme une somme d'opérateurs création et annihilation de champ :
Cela exprime un champ de bosons libres, où Ek est l'énergie cinétique. Cet hamiltonien est utilisé pour décrire des phonons.
Localisation
L'expérimentateur qui enregistre un « clic » dans son détecteur aimerait relier cet événement, qu'il interprète comme la détection d'une « particule » relativement bien localisée dans l'espace (et dans le temps), au champ quantique et à ses excitations, ce qui conduit au problème de la localisation en physique quantique relativiste. Pour certains types de « particules », l'opérateur de position de Newton-Wigner apporte des éléments de réponse.
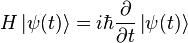
![\frac{1}{\sqrt{3}} \left[ \phi_1(r_1) \phi_2(r_2) \phi_2(r_3) + \phi_2(r_1) \phi_1(r_2) \phi_2(r_3) + \phi_2(r_1) \phi_2(r_2) \phi_1(r_3) \right]](https://static.techno-science.net/illustration/Definitions/autres/8/833350313ed2b1360d056ca0cb7d768c_d478eca41451c7a239d16bf9fc747132.png)