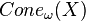Ultralimite - Définition

Propriétés de base des ultralimites

1. Si les (X_n,d_n) sont des espaces métriques géodésiques, alors est aussi géodésique.
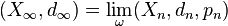
2. Si les (X_n,d_n) sont des espaces métriques complets, est également complet.
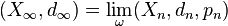
3. Si (X_n,d_n) est une suite d'espaces compacts qui converge (au sens de Hausdorff) vers un espace (X,d), ce qui implique que les (X_n,d_n) sont de diamètre uniformément borné, alors l'ultralimite est isométrique à (X,d).
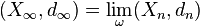
4. Si les (X_n,d_n)sont des espaces métriques propres, et si sont des points de base tels que la suite (X_n,d_n,p_n) converge (au sens de Hausdorff) vers un espace métrique propre (X,d), alors l'ultralimite est isométrique à (X,d).
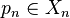
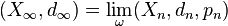
5. Soit κ≤0 and let (X_n,d_n) une suite de CAT(κ)-espaces. Alors l' ultralimite est aussi un CAT(κ)-espace.
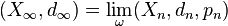
6. Soit (X_n,d_n) une suite de CAT(κ_n)-espaces, où Alors l'ultralimite est un arbre réel.

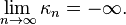
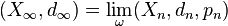
Exemples

1. Soit (X,d) un espace métrique compact ; posons (X_n,d_n)=(X,d) pour chaque . Alors l'ultralimite est isométrique à (X,d).
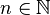
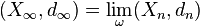
2. Soient (X,d_X) et (Y,d_Y) deux espaces métriques compacts distincts et soit (X_n,d_n)une suite telle que pour tout n on ait (X_n,d_n)=(X,d_X) ou (X_n,d_n)=(Y,d_Y). Soit et . Alors A₁, A₂ sont disjoints et Par conséquent, l'un des A₁, A₂ est de ω-mesure 1 et l'autre a pour ω-mesure 0. Donc est isométrique à (X,d_X) si ω(A₁)=1 et est isométrique à (Y,d_Y) si ω(A₂)=1. Cela montre que l'ultralimite peut dépendre du choix de l'ultrafiltre ω.
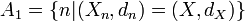
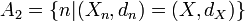
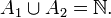
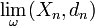
3. Soit (M,g) une variété riemannienne compacte connexe de dimension m, où g est une métrique riemannienne sur M. Soit d la métrique sur M correspondant à g ; (M,d) est alors un espace métrique géodésique. Choisissons un point de base p∈M. Alors l'ultralimite (et même la limite ordinaire au sens de Hausdorff) est isométrique à l'espace tangent T_pM de M à p, la distance sur T_pM étant donnée par le produit scalaire g(p). Ainsi, l'ultralimite est isométrique à l'espace euclidien muni de la distance usuelle.
4. Soit l'espace euclidien usuel à m dimensions. Alors le cône asymptotique est isométrique à .
5. Soit le réseau entier de dimension 2 avec la distance entre deux points du réseau donnée par la longueur du plus court chemin les reliant. Alors le cône asymptotique est isométrique à , où est la "distance de Manhattan" sur .
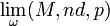
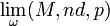
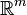
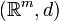
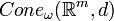
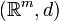
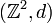
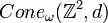
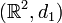
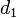
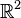
6. Soit (X,d) un espace métrique géodésique δ-hyperbolique, avec δ≥0. Alors le cône asymptotique est un arbre réel.
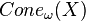
7. Soit (X,d) un espace métrique de diamètre fini. Alors est réduit à un point.
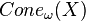
8. Soit (X,d) un CAT(0)-espace métrique. Alors est aussi un CAT(0)-espace.