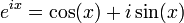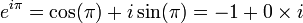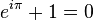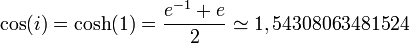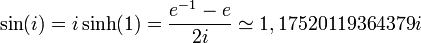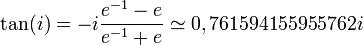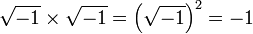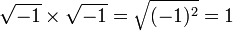Unité imaginaire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, l’unité imaginaire est un nombre complexe, noté i, dont le carré vaut − 1. Ses multiples par des nombres réels constituent les nombres imaginaires purs.
Constructions
Puisque tous les nombres réels ont un carré positif, l'unité imaginaire ne peut être considérée comme un point de la droite réelle. Il existe plusieurs façons de la définir.
Sa première apparition était sous la forme de
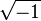
![\R[X]](https://static.techno-science.net/illustration/Definitions/autres/6/60ed190117e7614d227f8d1693161a5b_67a4b8800a94a9a175a1ac6f97f6cf7d.png)
- Si on prend X réel, X2 + 1 = 0 n'admet pas de solution.
- Si on imagine un nombre i tel que i2 = − 1, et qu'on exprime X = a + ib, alors l'équation X2 + 1 = 0 possède deux solutions : a = 0, b = 1 et a = 0, b = − 1. Autrement dit, la droite d'abscisses représentant les réels



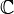
(Une représentation graphique complète de X2 + 1 dans le domaine complexe nécessiterait 4 dimensions : 2 pour X et 2 pour la valeur complexe de l'expression de X2 + 1.)
Le nombre imaginaire i est donc un outil mathématique pour apporter des solutions supplémentaires à certaines équations, en ajoutant une dimension aux nombres réels (remplacement d'une droite par un plan) ; les nombres comportant un multiple de cette unité imaginaire sont appelés nombres complexes.
i et la formule d'Euler
La formule d'Euler donne :
Où x est un nombre réel. La formule peut alors être analytiquement étendue pour un complexe z :
remplaçons x par π
et on obtient donc l'identité d'Euler :
C'est une équation remarquablement simple mettant en scène cinq nombres mathématiques très importants (0, 1, π, e et i) reliés uniquement par des additions, multiplications et exponentiations.
Propriétés de i
Son opposé est à la fois son inverse et son conjugué :
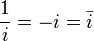
Ses images par les fonctions trigonométriques s'écrivent :
i est une racine de l'unité d'ordre 4, donc ses puissances sont
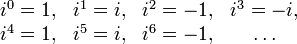
De plus, on peut se demander : pourquoi avoir noté cette unité i ?
Si on avait laissé la notion de
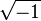
Mais aussi :
Et donc − 1 = 1, ce qui pose réellement problème. Ainsi, c'est presque deux siècles après l'apparition de l'unité imaginaire qu'Euler réforme l'écriture de ce nombre en posant : i2 = − 1