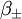Univers mixmaster - Définition

Introduction

L'univers mixmaster est une solution des équations de la relativité générale d'Einstein étudiée par Charles Misner en 1969. Elle décrit l'évolution temporelle d'un univers vide de matière, homogène mais anisotrope, dont le taux d'expansion diffère dans les trois directions d'espace. Ce modèle correspond au type IX de la classification de Bianchi. Il s'intéresse particulièrement à l'évolution de l'univers au voisinage d'une singularité gravitationnelle comme le Big Bang.

Discussion

Le modèle ressemble à l'univers de Friedmann-Lemaître-Robertson-Walker fermé, dans lequel les « tranches spatiales » sont positivement courbées et sont topologiquement des 3-sphères S³. Cependant, dans l'univers de FLRW, le S³ peut uniquement s'étendre ou se contracter : le seul paramètre dynamique est la dimension globale de S³, et paramétré par le facteur d'échelle a(t). Dans l'univers mixmaster, le S³ peut s'étendre ou se contracter, mais aussi se tordre da manière anisotrope. Son évolution est décrite par le facteur d'échelle a(t) aussi bien que par les deux paramètres de forme . Les valeurs des paramètres de forme décrivent les distorsions du S³ qui préservent son volume et qui maintiennent également un scalaire constant de la courbure du Ricci. Par conséquent, comme les 3 paramètres prennent des valeurs différentes, l'homogénéité est conservée, mais pas l'isotropie.

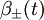
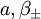
La dynamique de l'univers mixmaster se révèle extrêmement riche. Misner a notamment montré qu'au voisinage de la singularité gravitationnelle, l'univers s'étend dans deux et seulement deux directions, et se contracte le long de la troisième. Ce comportement est habituellement appelé singularité BKL, du nom de V. A. Belinsky, I. M. Khalatnikov et E. M. Lifschitz, qui l'ont étudiée en détail en 1970. Il a été conjecturé qu'il était générique à un phénomène d'effondrement gravitationnel. Il présente un certain nombre de caractéristiques d'un phénomène chaotique, notamment par le fait que la direction dans laquelle l'univers se contracte change de façon erratique au cours du temps, et que les différents taux d'expansion ou de contraction sautent d'une valeur à une autre de façon quasi aléatoire.

Applications à la cosmologie

Il espérait que le chaos barraterait et aplanirait l'Univers dans ses premiers instants. Aussi, durant les périodes dans lesquelles une direction était statique (i.e. : allant de l'expansion à la contraction), l'horizon de Hubble H ^{− 1} est infini dans cette direction. Il suggérait par là que le problème de l'horizon pouvait être résolu. Comme les directions de l'expansion et de la contraction varient, le problème de l'horizon serait résolu dans toutes les directions.

Tandis qu'il existait un exemple intéressant de chaos gravitationnel, il est largement reconnu que les problèmes cosmologiques que l'univers mixmaster tente de résoudre sont plus élégamment résolus par l'inflation cosmique. L'étude de la métrique de Misner est aussi connu sous le nom de métrique de Bianchi de type IX

Métrique

La métrique étudiée par Misner (légèrement modifiée pour sa notation) est donnée par :

.

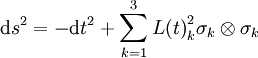
où les σ_k, considérés longtemps comme des formes différentielles, sont définis par :

σ₁ = sinψdθ − cosψsinθdφ,

σ₂ = cosψdθ + sinψsinθdφ,

σ₃ = − dψ − cosθdφ.

En termes de coordonnées (θ,ψ,φ), ceux-ci satisfont :

.

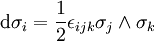
où d est la dérivée extérieure et , le produit wedge des formes différentielles. Cette relation rappelle les relations de commutation de l'algèbre de Lie de SU(2). Le groupe de variété pour SU(2) est la 3-sphère S³ et en vérité le σ_k décrit la métrique d'un S³ qui peut se tordre de manière anisotropique grâce à la présence de L_k(t).

Ensuite, Misner définit les paramètres Ω(t) et R(t) qui mesurent le volume des tranches spatiales, aussi bien que les « paramètres de forme » β_k par :

.

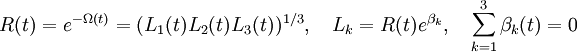
Comme il y a une codition sur les trois β_k, il ne devrait y avoir seulement que deux fonctions libres, qui Misner choisit comme étant , définie comme :

.

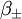
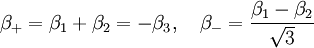
L'évolution de l'Univers est alors décrite en trouvant comme une fonction de Ω.