Théorème de d'Alembert-Gauss - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs est disponible ici.

Le théorème de d'Alembert-Gauss, simplement appelé théorème de d'Alembert ou encore théorème fondamental de l'algèbre, s'énonce de la façon suivante :

" Tout polynôme de degré supérieur ou égal à 1 à coefficients dans le corps $\mathbb C$ des nombres complexes a au moins une racine dans $\mathbb C$ ".

En d'autres termes, le corps $\mathbb C$ des nombres complexes est algébriquement clos. On en déduit facilement que tout polynôme de degré $n > 0$ est scindé, c'est-à-dire qu'il se factorise en produit de $n$ polynômes du premier degré : on dit qu'il a exactement $n$ racines (en tenant compte des ordres de multiplicité).

Ce théorème fut énoncé pour la première fois par Albert Girard. Jean le Rond d'Alembert en donna une démonstration presque complète, dans son Traité de dynamique. Carl Friedrich Gauss en donna la première démonstration rigoureuse au début du XIX^e siècle.

La dénomination " théorème fondamental de l'algèbre " fait sourire certains car il s'agit d'un théorème " exogène " à l'algèbre, au sens où l'on n'en connaît pas de démonstration qui évite de faire appel à des outils d'analyse.

Une preuve très concise repose sur le théorème de Liouville en analyse complexe. À cet effet, on considère un polynôme P à coefficients complexes, de degré au moins égal à 1. On suppose qu'il n'a aucune racine : dès lors, la fonction rationnelle 1 / P est entière et bornée (car elle tend vers 0 à l'infini) ; du théorème de Liouville, on déduit qu'elle est constante, ce qui contredit l'hypothèse sur le degré, et prouve ainsi par l'absurde l'existence d'au moins une racine de P.

Autre démonstration

Soit $P\,$ un polynôme de degré strictement positif à coefficients complexes.
Notons: $P(z) = a_0+a_1 z+\cdots+a_n z^n \,$ , pour $z\,$ dans $\mathbb C$ et $n width=$ 0 \," />.
D'après l'inégalité triangulaire, on a: 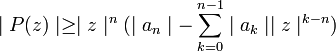$\mid P(z)\mid\geq\mid z\mid ^n(\mid a_n\mid - \sum_{k=0}^{n-1}\mid a_k\mid \mid z\mid ^{k-n}) \,$
On en déduit que: $\lim_{\mid z\mid \to +\infty} \mid P(z)\mid = +\infty$
Notons $m = inf_{z \in \mathbb C}\mid P(z)\mid$ . Il existe alors un réel $R\,$ tel que pour tout $z \in \mathbb C,\mid z\mid width=$ R," /> on a $\mid P(z) \mid width=$ 2 m \," />.
On en déduit que $m = inf_{\mid z\mid \leq R}\mid P(z)\mid$ .
Le disque $D(O,R)\,$ étant compact, il existe un nombre complexe $z_0\,$ de ce disque où la borne inférieure est atteinte. On a donc $m = \mid P(z_0)\mid$ . Il ne reste plus qu'à montrer que $m=0 \,$ pour terminer la démonstration.
Supposons que ce n'est pas le cas.
Notons $Q(z)=P(z_0+z)=b_0+b_1 z+\cdots+b_n z^n, pour z \in \mathbb C$
Soit $k\,$ le plus petit indice non nul tel que $b_k\neq0$ . Et soit $z_1\,$ une racine k-ième de $-b_k\,$ .
Notons: $b_0 = \mid P(z_0)\mid e^{i \theta}\,$ .
Alors pour $z=r^{\frac 1 k}\mid P(z_0)\mid^{\frac 1 k}z_1^{-1}e^{\frac {i\theta} k}$ où $r width=$ 0\," />, on a:
$Q(z)=b_0-b_0 r+\sum_{l=k+1}^n b_lz^l$
D'après l'inégalité triangulaire, on a:
$\mid Q(z)\mid \leq \mid b_0\mid \mid 1-r\mid + \mid \sum_{l=k+1}^n b_l z^l\mid$
Donc pour $0<r<1\,$ , on a:
$\mid Q(z)\mid - \mid b_0\mid \leq r(-\mid b_0\mid + \mid\sum_{l=k+1}^n b_lr^{\frac{l-k} k}z_1^{-l}\mid P(z_0)\mid^{\frac l k}e^{\frac{il\theta} k}\mid)$
Or quand $r \to 0$ tout en restant positif, le second membre devient strictement négatif car $\mid b_0\mid width=$ 0" />. Donc $\mid Q(z)\mid < \mid b_0 \mid = m$ . Ce qui est absurde d'après la définition de $m\,$ . $z_0\,$ est donc une racine de $P\,$ .