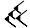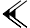Numération babylonienne - Définition
Cet article fait partie de la série Systèmes de numération |
|
| Notations | Notions |
|
|
| Numérations | |
| Additives | Positionnelles |
|
|
Les Babyloniens ont utilisé une grande variété de systèmes de numération : sexagésimal strict avec les clous et chevrons, décimal mélangeant du sexagésimal ou décimal. Pour une meilleure compréhension, on classe ici sous le terme de "Babyloniens" les Babyloniens, les Akkadiens et les Sumériens.
Numération sexagésimale
Les Babyloniens ont compté en base 60 (système sexagésimal) en utilisant une numération de position empruntée aux Sumériens. Il est à noter que cette base a traversé les siècles : on la retrouve aujourd'hui dans la notation des angles en degrés (360° = 6 x 60°) ou dans le découpage du temps (1 heure = 60 minutes = 60² secondes).
Chiffres
Des soixante chiffres du système sexagésimal, les Babyloniens en employaient 59 à l'exception du zéro. Ces chiffres étaient notés à l'aide d'un système additif décimal : un clou
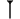
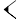
Voici la liste des chiffres de 1 à 60 :
-
-
Liste des chiffres cunéiformes babyloniens de 0 à 60. unités …0 …1
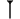
…2
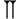
…3
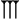
…4
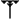
…5
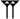
…6
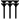
…7
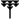
…8
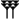
…9
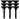
dizaines 0… ( 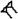
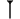
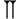
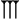
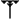
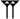
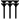
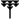
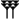
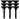
1… 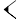
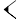
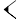
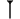
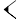
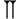
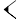
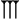
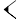
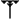
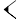
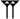
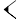
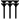
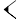
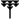
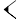
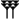
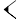
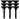
2… 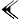
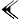
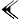
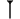
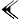
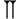
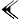
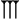
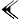
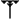
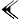
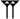
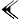
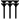
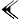
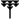
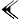
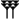
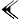
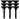
3… 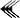
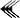
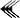
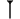
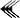
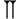
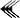
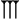
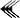
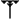
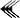
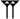
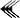
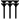
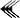
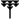
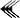
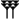
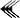
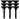
4… 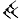
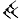
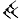
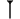
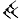
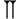
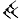
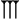
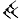
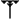
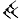
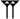
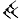
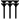
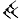
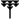
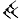
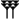
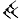
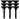
5… 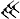
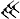
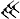
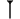
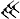
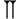
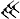
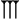
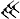
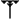
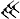
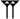
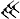
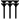
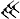
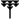
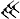
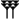
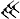
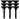
-
| Valeur décimale | Écriture babylonienne cunéiforme | Décomposition en base 60 |
|---|---|---|
| 1 |
|
1 = 1 x 1 |
| 17 |
|
17 = 17 x 1 |
| 44 |
|
44 = 44 x 1 |
| 60 |
|
60 = 1 x 60 + 0 x 1 |
| 85 |
|
1 × 60 + 25 x 1 |
| 3600 |
|
3600 = 1 x 60² + 0 x 60 + 0 x 1 |
| 11327 |
|
3 × 60² + 8 × 60 + 47 x 1 |
| 7000,2525 |
|
1 x 60² + 56 x 60 + 40 x 1 + 15/60 + 9/60² |
On remarquera que dans le tableau ci-dessus, les nombres 1, 60 et 3600 sont représentés de la même façon : bien que positionnel, le système babylonien ne note ni le zéro, ni la virgule comme dans la numération chinoise à bâtons. En un certain sens, la numération des Babyloniens ressemble à la notation scientifique avec mantisse et exposant, à ceci près que les Babyloniens ne notaient que la mantisse et conservaient l'exposant mentalement. En langage contemporain il s'agit de calcul en virgule flottante. Le lecteur des tablettes doit ainsi rétablir l'exposant des nombres qu'il déchiffre, ce qui rend l'interprétation parfois difficile. Pour noter le zéro, en position interne à un nombre, une espace puis le " 2 tourné " furent utilisés plus tardivement.
Numérations décimale et sexagésimale mélangées
Les chiffres sont construits sur la même base que ci-dessus, mis-à-part que l'on compte en base 10. Pour cela, quelques abréviations ont été ajoutées.
Liste des chiffres
|
|
Exemples
| Valeur | Nombres babyloniens |
|---|---|
| 44 |
|
| 85 |
|
| 327 |
|