Fonction zeta d'Hurwitz - Définition
En mathématiques, la fonction zeta d'Hurwitz est une des nombreuses fonctions zeta. Elle est définie comme suit :
-
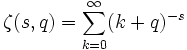
Elle s'étend par prolongement analytique à tout nombre complexe s différent de 1, et à tout nombre complexe q qui n'est pas entier négatif.
Quand q = 1, ceci coïncide avec la fonction Zeta de Riemann.
Relation avec les fonctions L de Dirichlet
En fixant un entier Q ≥ 1, les fonctions L de Dirichlet pour les caractères modulo Q sont des combinaisons linéaires, à coefficients constants, de
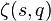
Précisément, soit
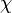
-
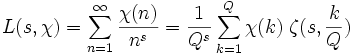
Formule d'Hurwitz
La formule d'Hurwitz est le théorème qui énonce
où
est une représentation de zeta qui est valide pour
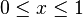
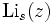
Relation avec les polynômes de Bernoulli
La fonction β définie ci-dessus généralise les polynômes de Bernoulli :
où
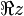
Relation avec la fonction polygamma
La fonction zeta d'Hurwitz généralise la fonction polygamma :
Relation avec fonction transcendante de Lerch
La fonction transcendante de Lerch généralise la fonction zeta d'Hurwitz :
et ainsi
Équation fonctionnelle
L'équation fonctionnelle relie les valeurs de la fonction zeta sur le coté gauche -et droit- du plan complexe. Pour les nombres entiers
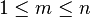
reste valable pour toutes les valeurs de s.
Série de Taylor
La dérivée partielle de la fonction zeta est une suite de Sheffer :
Ainsi, la série de Taylor peut être écrite comme suit :
Transformation de Fourier
La Transformée de Fourier discrète de la fonction zeta d'Hurwitz par rapport à l'ordre s est la fonction chi de Legendre.
Relation avec la fonction theta de Jacobi
Si
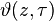
reste valable pour
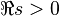
où

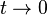
Bien que la fonction Zeta d'Hurwitz est vue par les mathématiciens comme relevant de la plus pure discipline des mathématiques, la théorie des nombres, elle apparaît aussi dans les statistiques appliquées ; voir la loi de Zipf et la loi de Zipf-Mandelbrot.
![\zeta(1-s,x)=\frac{1}{2s}\left[e^{-i\pi s/2}\beta(x;s) + e^{i\pi s/2} \beta(1-x;s) \right]](https://static.techno-science.net/illustration/Definitions/autres/0/08afc1b3685447f4fb7149c56ed8fd3f_7c88fcd645fe8b4347f82a4099291790.png)
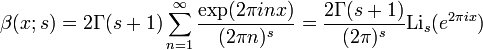
![B_n(x) = -\Re \left[ (-i)^n \beta(x;n) \right]](https://static.techno-science.net/illustration/Definitions/autres/f/fb05d128593f55353729151788e95b0b_92c327bc718b0d00fd48ac51a756b354.png)
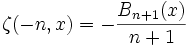
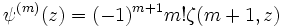
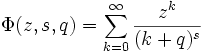
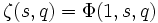
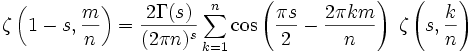
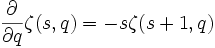
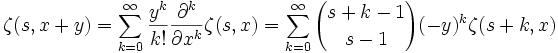
![\int_0^\infty \left[\vartheta (z,it) -1 \right] t^{s/2} \frac{dt}{t}= \pi^{-(1-s)/2} \Gamma \left( \frac {1-s}{2} \right) \left[ \zeta(1-s,z) + \zeta(1-s,1-z) \right]\,](https://static.techno-science.net/illustration/Definitions/autres/6/63a45442e9b287d065b92b8d9109c9d4_f18125b7d9ea62ad4f75e81d2252b3b7.png)
![\int_0^\infty \left[\vartheta (n,it) -1 \right] t^{s/2} \frac{dt}{t}= 2\ \pi^{-(1-s)/2} \ \Gamma \left( \frac {1-s}{2} \right) \zeta(1-s) =2\ \pi^{-s/2} \ \Gamma \left( \frac {s}{2} \right) \zeta(s)\,](https://static.techno-science.net/illustration/Definitions/autres/e/e1ba7ba3d5f1646239a63cd390c48661_05cfdde7e48ee34ec0f27e8c608f5399.png)

















































