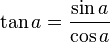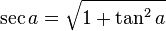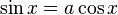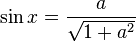Al-Battani - Définition

Al Battani

Al-Battani (env. 855-923) était un astronome et mathématicien arabe (on écrit aussi Al Batani, et en latin : Albategnius, Albategni, Albatenius ; nom complet : Ab? ?Abdull?h Mu?ammad ibn J?bir ibn Sin?n ar-Raqq? al-?arrani a?-?abi? al-Batt?n?), né à Harran près d'Urfa. Son épithète as-Sabi suggère que ses ancêtres étaient membres de la secte des Sabéens qui adoraient les étoiles, mais son nom complet affirme qu'il était musulman. On le désigne parfois comme le " Ptolémée des Arabes ".

Al-Battani a travaillé en Syrie, à Ar-Raqqa et à Damas où il est mort.

Son œuvre majeure, le Kit?b az-Z?j (le " Livre des tables ") composé de 57 chapitres, traduit en latin sous le titre de De Motu Stellarum par Platon de Tivoli (Plato Tiburtinus) en 1116 (imprimé en 1537 par Melanchthon, annoté par Regiomontanus), a considérablement influencé l'astronomie européenne. Une réédition apparut à Bologne en 1645. Le manuscrit original de Platon est conservé à la bibliothèque du Vatican. La bibliothèque de l'Escorial possède un manuscrit de chronologie astronomique d'al-Battani.

Astronomie

Il a corrigé certains calculs de Ptolémée et il a produit de nouvelles tables pour le Soleil et pour la Lune, qui ont longtemps fait autorité. Il a aussi traité la division de la sphère céleste. Il a découvert le mouvement de l'apogée du Soleil, calculé les valeurs de la précession des équinoxes (54.5" par an) et l'inclinaison de l'axe terrestre (23° 35').

Mathématiques

Probablement sans connaître les travaux de l'astronome indien du V^e siècle Âryabhata , il a introduit l'usage du sinus dans les calculs, et en partie celui de la tangente, formant ainsi les bases de la trigonométrie moderne.

Il a utilisé les idées d'al-Marwazi sur les tangentes (ou " ombres ") pour développer des méthodes de calcul des tangentes et des cotangentes, et il en a dressé des tables.

Il a créé plusieurs formules trigonométriques :

Il a aussi résolu l'équation

en la traduisant par l'équation suivante: