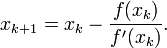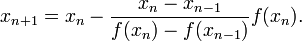Algorithme de recherche d'un zéro d'une fonction - Définition
Un algorithme de recherche d'un zéro d’une fonction est une méthode numérique ou un algorithme de recherche d’une valeur approchée d’un x vérifiant f(x) = 0, pour une fonction donnée f. Ici, x est un nombre réel appelé zéro de f ou lorsque f est polynomiale racine de f.
Lorsque x est un vecteur, les algorithmes pour trouver x tel que f(x) = 0 sont généralement appelés "algorithmes de résolution numérique d’une équation". Ces algorithmes sont une généralisation des algorithmes de recherche d’un zéro d’une fonction et peuvent s’appliquer à des équations linéaires ou non linéaires. Certains algorithmes de recherche des zéros (comme la méthode de Newton) peuvent être généralisés à la résolution numérique des équations non linéaires.
Les algorithmes de recherche des zéros d’une fonction sont étudiés en analyse numérique.
Algorithmes spécifiques
Dichotomie
L’algorithme le plus simple permettant de trouver des zéros est la méthode de dichotomie : on commence avec deux points a et b qui encadrent un zéro de la fonction, et à chaque itération, on choisit l’un des deux intervalles [a, c] ou [c, b], c = (a + b) / 2 étant le milieu de a et b. L’algorithme choisit toujours le sous-intervalle de [a, b] qui contient un zéro. La méthode de dichotomie garantit la convergence vers un zéro lorsque la fonction est continue. Sa progression dans la recherche est plutôt lente puisque sa vitesse de convergence est linéaire.
Newton-Raphson
La méthode de Newton, appelée aussi méthode de Newton-Raphson, " linéarise " la fonction f en la valeur approchée courante du zéro. Cela donne la relation récurrente :
La méthode de Newton peut ne pas converger si vous commencez trop loin d’un zéro. Cependant, si elle converge, elle est beaucoup plus rapide que la méthode de dichotomie (sa complexité est quadratique). La méthode de Newton est importante parce qu’elle peut aisément se généraliser à des problèmes en dimensions supérieures.
Sécante
Si nous remplaçons la dérivée de la fonction dans la méthode de Newton avec une différence finie, nous obtenons la méthode de la sécante. Elle utilise la relation récurrente
Ainsi, la méthode de la sécante ne requiert pas le calcul d’une dérivée, mais c’est au prix d’une vitesse de convergence lente (de l’ordre de 1,6).
Regula falsi
La méthode de la fausse position, aussi appelée méthode de regula falsi, s’apparente à la méthode de dichotomie. Cependant, elle ne coupe pas l’intervalle en deux parts égales à chaque itération, mais elle coupe l’intervalle en un point donné par la formule de la méthode de la sécante. La méthode de la fausse position hérite de la robustesse de la méthode de dichotomie et de la complexité " super-linéaire " de la méthode de la sécante.
Muller
La méthode de la sécante intervient également quand on approche la fonction inconnue f par interpolation linéaire. Quand une interpolation quadratique est employée à la place, cela donne la méthode de Müller. Elle converge plus rapidement que la méthode sécante. Une particularité de cette méthode est que le terme itéré xn peut devenir complexe.
Interpolation quadratique inverse
Cet inconvénient peut être évité par l'interpolation de la bijection réciproque de f ce qui mène à la méthode de l’interpolation quadratique inverse. Encore une fois, la convergence est asymptotiquement plus rapide que la méthode de la sécante, mais l'interpolation quadratique inverse se comporte souvent mal quand les itérés ne sont pas proches du zéro.
Brent
Enfin, la méthode de Brent est une combinaison de la méthode de dichotomie, de la méthode de la sécante et de l’interpolation quadratique inverse. À chaque itération, la méthode de Brent décide de laquelle de ces trois méthodes, est susceptible d’approcher au mieux le zéro, et effectue une étape en utilisant cette méthode. Cela donne une méthode robuste et rapide, très populaire et très appréciée.
Autres algorithmes
D’autres algorithmes de recherches de zéros sont
- Successive substitutions
- méthode de Broyden
- méthode du point fixe
Von Mises
Gradient conjugué
La méthode du gradient conjugué
Recherche des racines d’un polynôme
Une attention particulière a été donné au cas particulier où la fonction f est polynomiale. Bien sûr, les méthodes décrites dans la section précédente peuvent être utilisées. En particulier, il est facile de déterminer la dérivée d’un polynôme, et la méthode de Newton représente un très bon candidat. Mais il est possible de choisir une méthode qui exploite le fait que f est un polynôme.
Une possibilité est de considérer la matrice compagnon associée au polynôme. Sachant que les valeurs propres de cette matrice coïncident avec les racines du polynôme, on peut alors utiliser n’importe quel algorithme de recherche de valeur propre pour trouver des valeurs approchées des racines du polynôme initial.
Une autre possibilité est d’utiliser la méthode de Laguerre, qui est une méthode très compliquée mais qui converge très rapidement. En fait, elle développe une vitesse de convergence cubique pour les racines simples, pulvérisant la vitesse de convergence quadratique de la méthode de Newton.
Si le polynôme a des coefficients rationnels et si on recherche uniquement des racines rationnelles, alors la méthode de Ruffini peut être utilisée.
Dans tous les cas, il faut garder à l’esprit que le problème de recherche de valeurs approchées de racines peut être mal conditionné comme le montrent les polynômes de Wilkinson.