Arbelos - Définition

L'arbelos est une figure géométrique plane étudiée , entre autres, par Archimède(-287 - -212, Syracuse). Le terme " arbelos " signifie couteau du savetier.

Construction

Soit un demi-cercle de diamètre horizontal BC. Soit A un point quelconque de ce diamètre.

• Tracer le demi-cercle de diamètre BA intérieur.
• Tracer le demi-cercle de diamètre AC intérieur.
• Griser la surface intérieure obtenue : c'est une lame d'arbelos.

Propriétés

Cette figure possède de nombreuses propriétés dont voici quelques-unes:

Propriété de l'aire : soit AH la demi-corde verticale passant par A . L'aire de l'arbelos est égale à l'aire du cercle de diamètre AH.

Démonstration : il suffit d'appeler b et c les diamètres AB et AC, et h la hauteur AH. Les aires des demi-cercles sont alors respectivement de , , . Puis, par différence, on obtient l'aire de l'arbelos . La dernière étape fait appel aux propriétés du triangle rectangle dans lequel le carré de la hauteur est égal au produit des longueurs découpées sur l'hypoténuse. En d'autres termes : bc = h². Ce qui nous donne pour l'aire de l'arbelos : qui est bien l'aire du cercle de diamètre AH

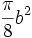
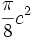
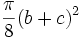
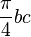
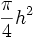
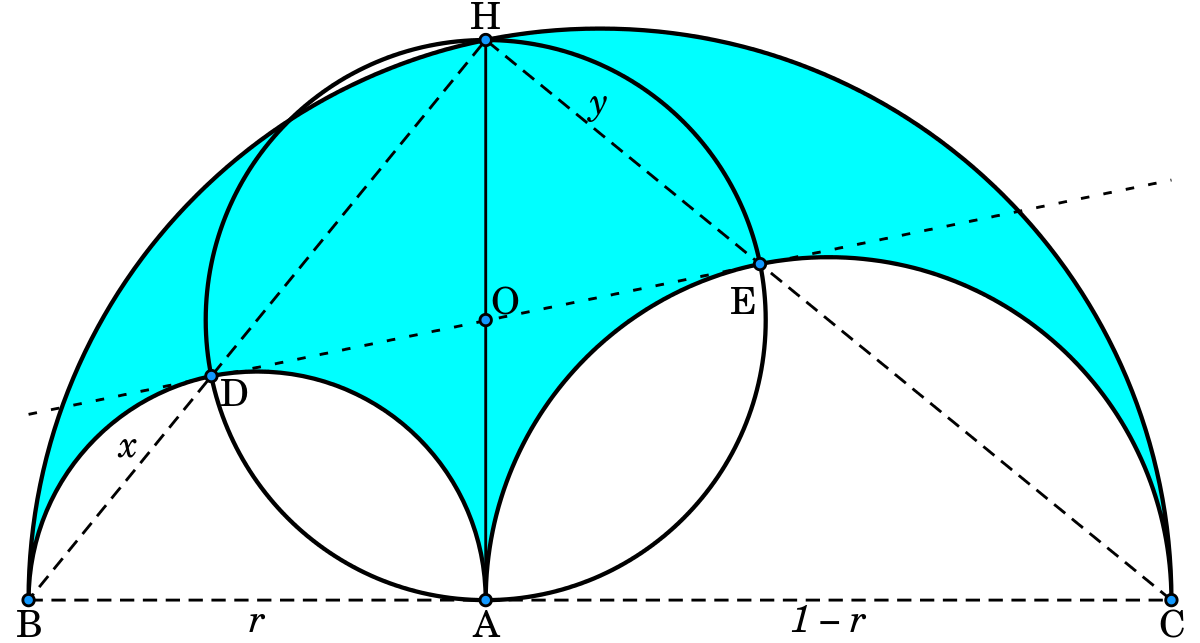
Propriété du rectangle: Le segment BH coupe le demi-cercle BA en D. Le segment CH coupe le demi-cercle AC en E. Alors DHEA est un rectangle

Démonstration : Les triangles BDA, BHC et AEC sont rectangles car inscrits dans des demi-cercles (théorème de Thalès (cercle). Le quadrilatère ADHE possède donc trois angles droits, c'est un rectangle.

Propriété des tangentes : La droite (DE) est une tangente commune aux deux cercles.

Démonstration : La similitude de centre D qui envoie B sur A a pour angle π / 2 et envoie aussi A sur H (les triangles DBA et DAH sont semblables). Elle envoie donc le milieu I de [AB] sur le milieu O de [AH] et l'angle IDO est droit. La droite (DO) est donc tangente au premier cercle en D. Comme ADHE est un rectangle, le point O est sur (DE) donc (DE) est une tangente du premier cercle. Elle est tangente du second par un raisonnement analogue.