Archimédien - Définition

A l'origine, l'énoncé de l'axiome d'Archimède est le suivant : " Pour deux grandeurs inégales, il existe toujours un multiple entier de la plus petite, supérieur à la plus grande. "

On appelle archimédien des structures dont les éléments vérifient une propriété comparable.

Groupe

Soit (G,+,≤) un groupe commutatif totalement ordonné.

(G,+,≤) vérifie l'axiome d'Archimède ou est archimédien si et seulement si :

quels que soient les éléments a > 0 et b ≥ 0 de G ,  il existe un entier naturel n tel que n × a ≥ b.

Anneau

Soit (A,+,×,≤ ) un anneau totalement ordonné.

(A,+,×,≤) vérifie l'axiome d'Archimède ou est archimédien si et seulement si le groupe commutatif (A,+,≤) lui-même est archimédien.

Corps

Soit (K,+,×,≤) un corps totalement ordonné.

(K,+,×,≤) vérifie l'axiome d'Archimède ou est archimédien si et seulement si le groupe commutatif (K,+,≤) lui-même est archimédien. Un tel corps est un sous-corps du corps des réels (R,+,×,≤)

Remarques

Cet axiome intervient également comme l'axiome IV,1 du " groupe IV de continuité " dans l'axiomatique de la géométrie euclidienne proposée par Hilbert en 1899. Hilbert montre par exemple que la preuve de l'égalité des aires entre deux parallélogrammes de même base et de même hauteur utilise nécessairement l'axiome d'Archimède.

Hilbert montre également que, dans un corps, si on ne suppose pas la multiplication commutative, alors nécessairement, cette commutativité du produit découle du caractère archimédien du corps. Pour montrer que ab = ba, l'idée est de prendre un élément d arbitrairement petit, et d'utiliser le caractère archimédien du corps pour encadrer a entre nd et (n+1)d et encadrer b entre md et (m+1)d, pour deux entiers m et n. On utilise cet encadrement pour en déduire un encadrement arbitrairement petit de ab-ba et conclure que cette différence est nulle.

Exemples

Exemple 1

( ,+,×,≤) et ( ,+,×,≤) sont des corps archimédiens.

Exemple 2

Voici un exemple d'anneau non archimédien. Considérons l'anneau des polynômes sur . Un polynôme est caractérisé par la suite de ses coefficients (a₀, ..., a_n, ...), nulle à partir d'un certain rang.

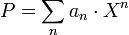
Si le polynôme Q admet pour coefficients (b₀, ..., b_n, ...), nous dirons que :

P < Q si et seulement s’il existe k ≥ 0 tel que, pour tout p < k, a_p = b_p et a_k < b_k

P ≤ Q si et seulement si P < Q ou P = Q

(Il s'agit de l'ordre lexicographique sur les coefficients des polynômes)

Alors ( ,+,×,≤) est un anneau totalement ordonné, mais qui n'est pas archimédien. En effet, pour tout n entier, on a 0 < nX < 1.

Pour l'ordre indiqué, X est un " infiniment petit ".

Bibliographie

David Hilbert : les fondements de la géométrie, Dunod, Paris 1971 ou Gabay, 1997