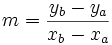Pente (mathématiques) - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
La pente est le coefficient directeur dans un repère cartésien orthonormé.
En géométrie cartésienne, le coefficient directeur désigne le coefficient a de l'équation d'une droite, y = ax + b. Cette quantité représente la variation de l'ordonnée y lorsque l'abscisse x augmente d'une unité. (On notera que cette définition exclut les droites parallèles au deuxième axe de coordonnée).
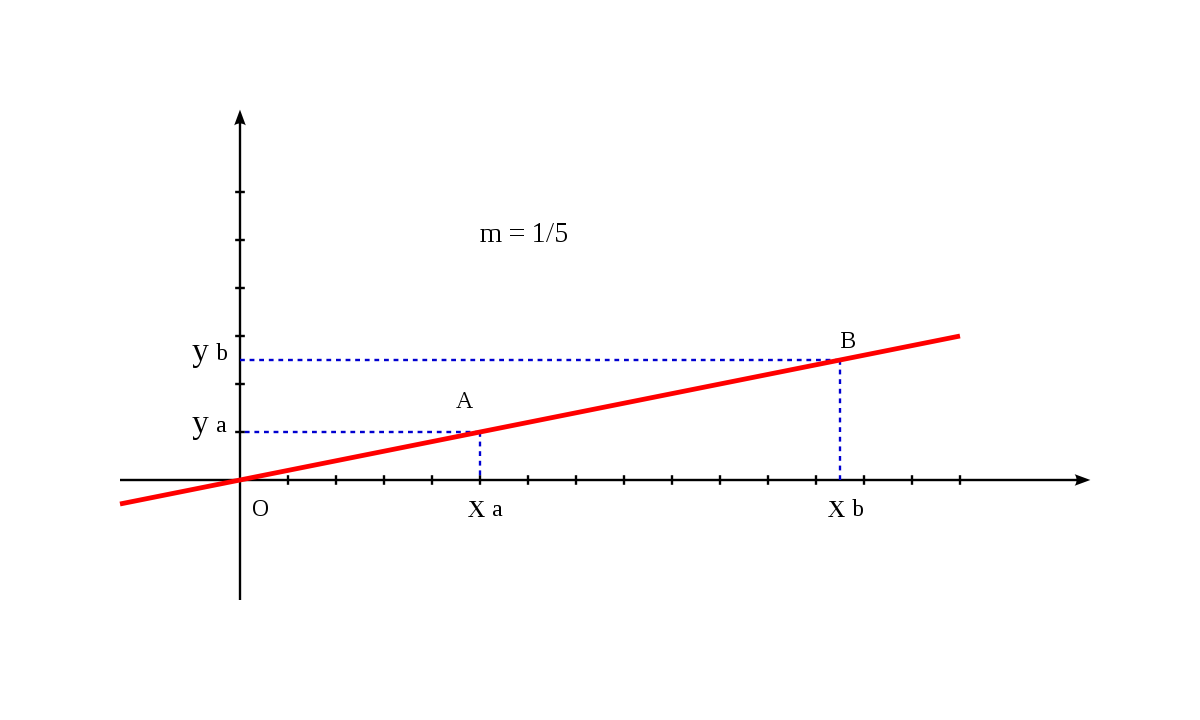
La pente d'une droite (non parallèle à l'axe Oy) correspond au rapport entre la variation de y et la variation correspondante de x. Cela correspond donc également à la tangente de l'angle que fait la droite avec l'axe Ox. En physique, l'axe Ox étant interprété comme un axe horizontal, la pente représente le rapport entre la distance verticale et la distance horizontale lorsqu'on suit le mouvement d'un point sur la droite. Cette pente peut être exprimée par un pourcentage : une pente de 20% correspond par exemple à un coefficient directeur de 1/5.
Si une fonction réelle est dérivable en un point, sa courbe représentative admet une tangente en ce point dont la pente est égale à la dérivée de la fonction.
Calcul du coefficient directeur d'une droite déterminée par deux de ses points
Soit une droite (non parallèle à l'axe Oy), dont on connaît deux points distincts A (xa,ya) et B (xb,yb). Le coefficient directeur m de cette droite vaut :