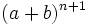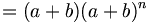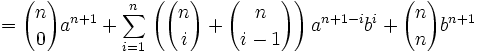Triangle de Pascal - Définition
En mathématiques, le triangle de Pascal est un arrangement géométrique des coefficients binomiaux dans un triangle. À la ligne i et à la colonne j (0 ≤ j ≤ i) est placé le coefficient binomial
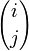
| 1 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | |||||||||
| 1 | 2 | 1 | ||||||||
| 1 | 3 | 3 | 1 | |||||||
| 1 | 4 | 6 | 4 | 1 | ||||||
| 1 | 5 | 10 | 10 | 5 | 1 | |||||
| 1 | 6 | 15 | 20 | 15 | 6 | 1 | ||||
| 1 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | |||
| 1 | 8 | 28 | 56 | 70 | 56 | 28 | 8 | 1 | ||
| 1 | 9 | 36 | 84 | 126 | 126 | 84 | 36 | 9 | 1 | |
| 1 | 10 | 45 | 120 | 210 | 252 | 210 | 120 | 45 | 10 | 1 |
Utilisations
Polynômes
Le triangle de Pascal est souvent utilisé dans les développements binomiaux. Par exemple
- (X + 1)2 = 1X2 + 2X + 12
Notez que les coefficients de chaque monôme, sont ceux de la troisième ligne du triangle de Pascal, c'est-à-dire 1, 2, 1. Ainsi quand nous effectuons un développement de la forme
-
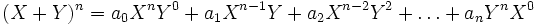
les coefficients sont ceux qui se trouvent sur la n+1ème ligne du triangle de Pascal.
Sommations
Connaissant la formule de sommation
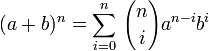
Posons a = b = 1, on a alors
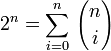
Posons a = 1 et b = -1, on a alors
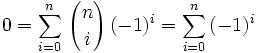
Connaissant ces deux égalités, dont l'une est une somme alternée, il vient que la somme des termes d'ordre 0, 2, 4,... dans une rangée est 2n − 1
Dénombrement
Le nombre d'une colonne x (en comptant à partir de 0 les colonnes) et d'une ligne y (en comptant à partir de 0 les lignes) indique le nombre de permutations possibles.
Nombres de Catalan
À partir du triangle, il existe plusieurs façons de calculer les nombres de Catalan. La plus simple est de prendre une rangée d'ordre impair et de soustraire les troisième et premier termes, sachant que la série commence par 1, 1, 2 :
6 - 1 = 5
15 - 1 = 14
28 -1 = 27
...
Ces nombres interviennent dans divers problèmes géométriques discrets.
Construction
Combinatoire
En écrivant la formule de Pascal,
- pour tous entiers i et j tels que 0 < j < i,
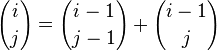
nous remarquons que le coefficient de la ligne i et colonne j s'obtient en ajoutant les coefficients de la ligne i - 1 et colonne j - 1 et de la ligne i - 1 et colonne j. De plus nous savons que
-
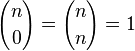
Nous en déduisons une méthode de construction du triangle de Pascal :
- nous plaçons dans la colonne 0 des 1 à chaque ligne, et des 1 à chaque entrée de la diagonale,
- en partant du haut et en descendant, nous complétons le triangle en ajoutant deux coefficients adjacents d'une ligne, pour produire le coefficient de la ligne inférieure, en dessous du coefficient de droite.
Démonstration
Cette formule se démontre simplement par récurrence :
hypothèse de récurrence:
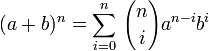
Cette hypothèse est vraie au rang 1 :
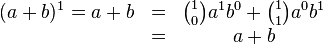
Montrons que si elle est vraie pour n alors elle est vraie pour n+1:
|
|
|
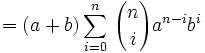
|
|
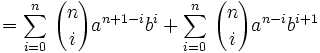
|
|
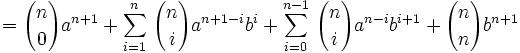
|
|
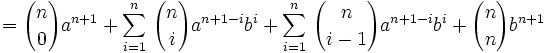
|
|
|
|
|
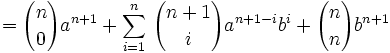
|
|
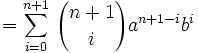
|
La formule est vraie au rang n+1, elle est donc vraie pour tout n.
Matricielle
Facile à construire à partir des factorielles, il est possible de représenter le triangle de Pascal à l'aide de l'exponentielle d'une matrice : le triangle est le résultat de l'exponentielle d'une matrice dont la sous-diagonale contient 1, 2, 3, 4, …, zéro ailleurs.
Informatique
Écrivons l'algorithme, en langage formel, de construction du triangle de Pascal. Notez que cet algorithme crée une nouvelle ligne à partir de la précédente.
Variables:
Tableau de 1 à 50 de tableau de 1 à 50 d'entiers c (tableau bidimensionnel)
Entiers i, j, n
n ← 10 c(lien)(lien) ← 1 pour i de 1 à n faire c[i](lien) ← 1 c[i][i] ← 1 pour j de 1 à i-1 faire c[i][j] ← c[i-1][j-1] + c[i-1][j]
afficher_tableau(c)
Généralisations
La formule du binôme généralisé est une importante généralisation du triangle de Pascal, car elle permet de manipuler des nombres complexes dans la base, tout comme d'utiliser des exposants complexes.
Le triangle de Pascal se généralise aisément à des dimensions supérieures. La version tridimensionnelle s'appelle la pyramide de Pascal.
Curiosités
Dans ce triangle, si tous les nombres pairs sont coloriés en blanc et tous les nombres impairs en noir, le triangle de Sierpinski apparaît.
Histoire
Le triangle a été décrit par Zhu Shijie en 1303 dans son livre Le Miroir de jade des quatre inconnues. Dans ce livre, Zhu présente le triangle comme une méthode ancienne (de plus 200 années avant son temps) pour déterminer les coefficients du binôme, ce qui indique que la méthode était connue des mathématiciens chinois cinq siècles avant Pascal. Elle était également connue des mathématiciens persans, par exemple al-Karaji (953 - 1029) ou Omar Khayyam au XIe siècle.