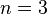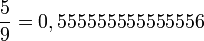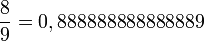Calcul intégral - Définition
Cet article fait partie de la série Mathématiques élémentaires |
| Algèbre |
| Analyse |
| Arithmétique |
| Géométrie |
| Logique |
| Probabilité |
| Statistique |
Le calcul intégral est la deuxième des idées du calcul infinitésimal.
Primitives
Soit









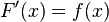
Théorème :
Si










Par exemple, si

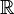
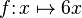

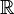
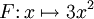



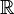
Un autre exemple, si


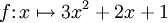


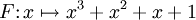

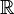
Remarque :
Soit


Si



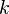
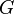

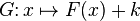


Nous en déduisons que si


Proposition :
Deux primitives d’une fonction diffèrent d’une constante.
En effet soit



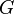

Nous avons
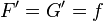
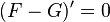

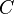

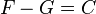
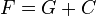
Ensemble des primitives d’une fonction sur un intervalle
Soit


Si





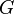
où
Par exemple, si

- pour tout réel

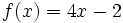
alors la fonction

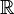
- pour tout réel

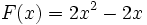
est une primitive de

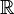

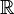
où
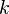
Conséquences :
- La fonction nulle sur un intervalle


- Soit




Il existe une et une seule primitive


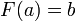



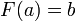
Question :
Soit

- pour tout réel

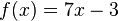
Quelle est la primitive de

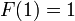
Réponse:
On calcule d'abord la forme générale des primitives de

- une primitive de
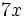
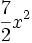
- une primitive de
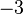
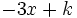
- la forme générale recherchée est
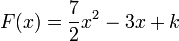
Reste maintenant à trouver la valeur de
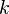
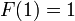
On résout l'équation
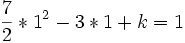
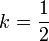
Conclusion :
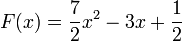
Intégrale
Définition de l’intégrale à partir de la notion de primitive
Soit












qui ne dépend pas du choix de la primitive de



qui se lit " intégrale de



qui se lit "



Dans la notation avec le symbole ?,
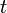
-
-
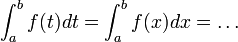
-
de plus le nombre représenté par cette intégrale ne dépend pas de
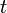
Remarquons dans le cas où


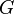

n’est autre que la primitive de


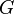

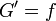
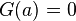
Nous avons donc
Propriétés de l’intégrale
Linéarité de l'intégrale
Si

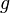


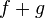




De plus, si
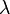
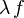

Relation de Chasles
Soient










-
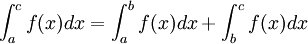
En effet si



-
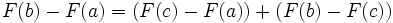
En prenant
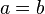
en effet
Positivité de l’intégrale
Soit






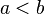
Si pour tout réel

![\left [a, b \right ]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
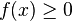
En effet sous cette condition, toute primitive de


Conséquences :
Croissance de l’intégrale
Si

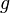


![\left[a, b \right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
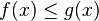
(il suffit de poser
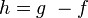
Inégalité de la moyenne
S’il existe
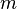
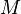

![\left[a, b\right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
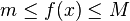
S’il existe un réel
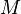

![\left[a, b\right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
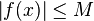
S’il existe un réel
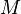


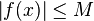



Forme simple du premier théorème de la moyenne
Si








Valeur moyenne d'une fonction
Si








![\left[a, b\right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
Parité
Soit




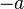

- si

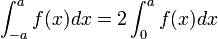
- si

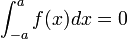
Intégrale et aire
Un cas particulier :
Soient


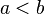

![\left[a, b\right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)

- pour tout réel

![\left[a, b\right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
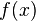

Alors l’intégrale de



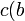
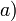
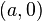
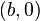
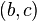
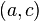
Théorème :
Soient


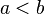

![\left[a, b\right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
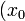
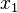
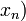
![\left[a, b\right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
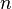
Nous avons alors pour tout
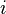
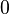
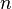
Alors la somme
tend vers
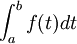
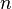
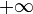
Interprétation graphique :
Cette somme (appelée somme de Riemann) représente graphiquement la somme algébrique des aires des rectangles de gauche et est une valeur approchée de
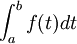
Si

![\left[a, b\right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)

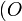
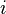
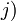
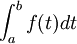
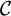
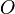





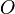

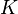
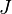
Méthodes de calcul d'une intégrale
Calcul direct à l'aide des primitives usuelles
Intégration par parties
Théorème :
Soit


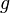

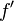
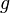

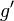





En particulier :
Théorème :
Soient


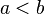

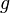
![\left[a, b\right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
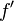
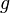

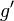
![\left[a, b\right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
On peut généraliser cette formule aux fonctions de classe Ck + 1
Intégration par la méthode des résidus
Calcul numérique approché d'une intégrale
On considère ici le cas d'une fonction

![\left [a, b \right ]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
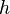
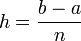
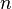
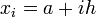
Méthode des rectangles
La méthode des rectangles revient à une approximation de

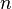
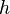
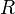
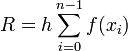
Méthode des trapèzes
On utilise une fonction continue affine par morceaux approchant la fonction à intégrer et égale à celle-ci sur les points de la subdivision en
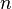
![\left[ a , b \right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
![\left[ a , b \right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
En remplaçant par des trapèzes les rectangles utilisés précédemment, on obtient :
![R = h\left[ \frac{f(a)+f(b)}{2} + \sum_{i=1}^{n-1} f(x_i) \right]\,](https://static.techno-science.net/illustration/Definitions/autres/0/0ffc6152bf5247b20a232027c1e41f68_c245ee3ec1f950fd405623dd48145fdf.png)
On peut déterminer la précision de cette approximation en utilisant la formule suivante :
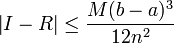
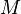

![[a;b]\,](https://static.techno-science.net/illustration/Definitions/autres/d/d21f69511ca60f3abd84c78449fef37c_bceb603f06c385a9bad577a063314623.png)

Méthode de Simpson
On utilise maintenant des paraboles que l'on fait passer par trois points consécutifs du découpage en
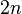

On s'appuie sur le résultat exact suivant où
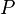
Si



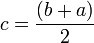
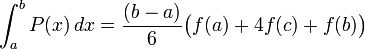

![R = \frac{h}{6} \left[ f(a) + f(b) + 4 \sum_{i=0}^{n-1}f(x_{2i+1}) + 2 \sum_{i=1}^{n-1} f(x_{2i}) \right]\,](https://static.techno-science.net/illustration/Definitions/autres/f/fe1bd66b54b764bcf17b0e3dd7211180_c36f560970d987258882d9a4ddb2a110.png)
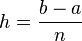
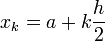
On peut ici aussi déterminer la précision de la méthode, avec la formule suivante :
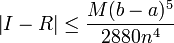
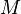

![[a;b]\,](https://static.techno-science.net/illustration/Definitions/autres/d/d21f69511ca60f3abd84c78449fef37c_bceb603f06c385a9bad577a063314623.png)

Méthode de Gauss-Legendre
On utilise aussi en analyse numérique une méthode basée sur l'orthogonalité des polynômes de Legendre. pour le produit scalaire
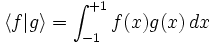
Elle est appelée méthode de Gauss-Legendre, et permet de calculer avec une grande précision les intégrales de fonctions suffisamment régulières sur un segment
![\left[ a , b \right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
Il suffit de réaliser une application affine de
![\left[ a , b \right]\,](https://static.techno-science.net/illustration/Definitions/autres/3/306000b4d4732ac8ef6254abda3a9776_25f0875c0fcafb9d19388882eb5d45ee.png)
![\left[ -1 , +1 \right]\,](https://static.techno-science.net/illustration/Definitions/autres/6/6033617927755bc39f68edd671632201_295de994ef0db3a52dfdaa44901c0345.png)
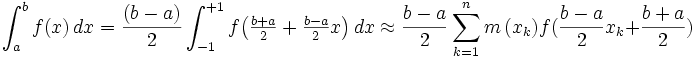
où
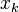
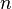
et où
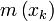
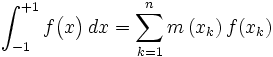
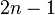
Les premiers polynômes sont
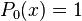
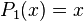
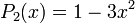
...
Une excellente précision est garantie dès que
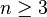
Exemple
| Numéro | Abscisse | Poids |
|---|---|---|
| 1 |
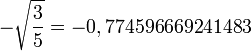
|
|
| 2 |
|
|
| 3 |
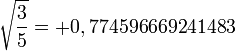
|
|
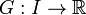
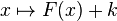
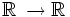
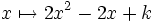
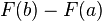
![\left[F(t)\right]_a^b\,](https://static.techno-science.net/illustration/Definitions/autres/e/efb7211da49ec3eb321d68fcf9f62268_f64d3d39a9514d0302523fe3aea92069.png)
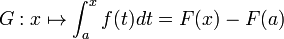
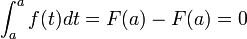
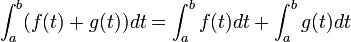
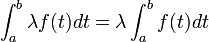
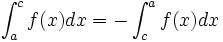
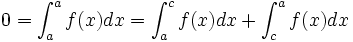
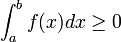
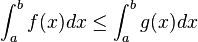
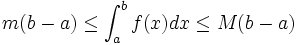
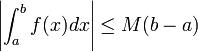
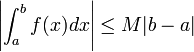
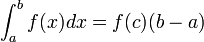
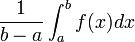
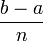
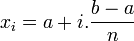
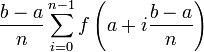
![\int_a^x f^{\prime}\left( t\right) g\left( t\right) dt=\left[f\left( t\right) g\left( t\right)\right]_a^x -\int_a^x f\left( t\right) g^{\prime }\left( t\right) dt\,](https://static.techno-science.net/illustration/Definitions/autres/2/21825efec9933c343afb12a5ecb7d411_2b28e662e1b3c715dd9a88274ea97285.png)
![\int _{a}^{b}f^{\prime}\left( t\right) g\left( t\right) dt=\left[ f\left( t\right) g\left( t\right) \right] _{a}^{b}-\int _{a}^{b}f\left( t\right) g^{\prime }\left( t\right) dt\,](https://static.techno-science.net/illustration/Definitions/autres/c/c03f613531c8737ed6b667815e26eb20_a2101cbd577ff4bd6b5c2f455a2fbd63.png)
![\int_{a}^{b} f^{k+1}(x) g(x)\,dx = \left[ \sum_{n=0}^{k}(-1)^{n} f^{k-n}(x) g^{n}(x) \right]_{a}^{b} + (-1)^{k+1} \int_{a}^{b} f(x) g^{k+1}(x) \,dx](https://static.techno-science.net/illustration/Definitions/autres/3/3372ebf0d23a68aa546c4a225ab84664_39b7df136aa0c1b81cf55bcd565257e2.png)