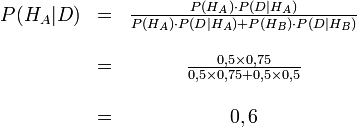Inférence bayésienne - Définition
On nomme inférence bayésienne la démarche logique permettant de calculer ou réviser la probabilité d'une hypothèse. Cette démarche est régie par l'utilisation de règles strictes de combinaison des probabilités, desquelles dérive le théorème de Bayes. Dans la perspective bayésienne, une probabilité n'est pas interprétée comme le passage à la limite d'une fréquence, mais plutôt comme la traduction numérique d'un état de connaissance (le degré de confiance accordé à une hypothèse, par exemple; voir théorème de Cox-Jaynes).
Jaynes utilisait à ce sujet avec ses étudiants la métaphore d'un robot à logique inductive. On trouvera un lien vers un de ses écrits dans l'article Intelligence artificielle.
La manipulation des probabilités : notation et règles logiques
L'inférence bayésienne est fondée sur la manipulation d'énoncés probabilistes. Ces énoncés doivent être clairs et concis afin d'éviter toute confusion. L'inférence bayésienne est particulièrement utile dans les problèmes d'induction. Les méthodes bayésiennes se distinguent des méthodes dites standard par l'application systématique de règles formelles de transformation des probabilités. Avant de passer à la description de ces règles, familiarisons-nous avec la notation employée.
Notation des probabilités
Prenons l'exemple d'une femme cherchant à savoir si elle est enceinte. On définira d'abord une hypothèse E : elle est enceinte, dont on cherche la probabilité p(E). Le calcul de cette probabilité passe évidemment par l'analyse du test de grossesse. Supposons que des études aient démontré que pour des femmes enceintes, le test indique positif 9 fois sur 10. Pour les femmes non-enceintes, le test indique négatif dans un ratio de 19/20. Si l'on définit les hypothèses :
- TP : le test est positif,
- TN : le test est négatif,
on peut interpréter les résultats précédents de manière probabiliste :
La probabilité de l'hypothèse TP sachant que la femme est enceinte est de 0,9.
En langage des probabilités, cet énoncé sera décrit par l'expression p(TP | E) = 0,9. De la même manière
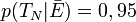
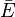
En plus de l'opérateur conditionnel |, les opérateurs logiques ET et OU ont leur notation particulière. Ainsi, la probabilité simultanée de deux hypothèses est notée par le signe
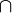
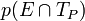
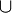
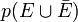
Les règles de la logique des probabilités
Il existe seulement deux règles pour combiner les probabilités, et à partir desquelles est bâtie toute la théorie de l'analyse bayésienne. Ces règles sont les règles d'addition et de multiplication.
La règle d'addition
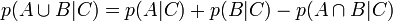
La règle de multiplication
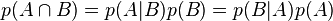
Le théorème de Bayes peut être dérivé simplement en mettant à profit la symétrie de la règle de multiplication
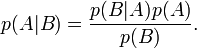
Le théorème de Bayes permet d'inverser les probabilités. C'est-à-dire que si l'on connaît les conséquences d'une cause, l'observation des effets permet de remonter aux causes.
Dans le cas précédent de la femme enceinte, sachant le résultat du test, il est possible de calculer la probabilité que la femme soit enceinte en utilisant le théorème de Bayes. En effet, dans le cas d'un test positif,
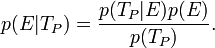
- C'est cette estimation a priori qui est systématiquement ignorée par les méthodes statistiques standard.
Notation d'évidence
Cette notation est souvent attribuée à I. J. Good. Ce dernier en attribuait cependant la paternité à Alan Turing et, indépendamment, à d'autres chercheurs dont Jeffreys.
Dans la pratique, quand une probabilité est très proche de 0 ou de 1, il faut observer des éléments considérés eux-mêmes comme très improbables pour la voir se modifier. Pour mieux fixer les choses, on travaille souvent en décibels (dB), avec l'équivalence suivante :
Ev(p) = 10 log10 p/(1-p).
Une probabilité de -40 dB correspond à une probabilité de 10-4, etc. L'intérêt de cette notation, outre qu'elle évite de manier trop de décimales au voisinage de 0 et de 1, est qu'elle permet aussi de présenter la règle de Bayes sous forme additive : il faut le même poids de témoignage (weight of evidence) pour faire passer un évènement d'une plausibilité de -40dB (10-4) à -30dB (10-3) que pour le faire passer de -10dB (0,1) à 0dB (0,5), ce qui n'était pas évident en gardant la représentation en probabilités. La table suivante présente quelques équivalences :
Probabilité Evidence (dB) Evidence (bits) 0.0001 -40.0 -13.3 0.0010 -30.0 -10.0 0.0100 -20.0 -6.6 0.1000 -9.5 -3.2 0.2000 -6.0 -2.0 0.3000 -3.7 -1.2 0.4000 -1.8 -0.6 0.5000 0.0 0.0 0.6000 1.8 0.6 0.7000 3.7 1.2 0.8000 6.0 2.0 0.9000 9.5 3.2 0.9900 20.0 6.6 0.9990 30.0 10.0 0.9999 40.0 13.3
Ev est une abréviation pour weight of evidence, parfois traduit en français par le mot évidence ; la formulation la plus conforme à l'expression anglaise d'origine serait le mot à mot poids de témoignage, mais par une coïncidence amusante "évidence" se montre très approprié en français pour cet usage précis.
C'est peu après les publications de Jeffreys qu'on découvrit qu'Alan Turing avait déjà travaillé sur cette question en nommant les quantités correspondantes log-odds dans ses travaux personnels.
Comparaison avec la statistique classique
Différence d'esprit
Une différence entre l'inférence bayésienne et les statistiques classiques, dites aussi fréquentistes, indiquée par Myron Tribus, est que
- les méthodes bayésiennes utilisent des méthodes impersonnelles pour mettre à jour des probabilités personnelles, dites aussi subjectives (une probabilité est en fait toujours subjective, lorsqu'on analyse ses fondements),
- les méthodes statistiques utilisent des méthodes personnelles pour traiter des fréquences impersonnelles.
Les bayésiens font donc le choix de modéliser leurs attentes en début de processus (quitte à réviser ce premier jugement à l'aune de l'expérience au fur et à mesure des observations), tandis que les statisticiens classiques se fixaient a priori une méthode et une hypothèse arbitraires et ne traitaient les données qu'ensuite (ce qui avait tout de même le mérite de bien alléger les calculs).
Quand utiliser l'une ou l'autre ?
Les deux approches se complètent, la statistique étant en général préférable lorsque les informations sont abondantes et d'un faible coût de collecte, la bayésienne dans le cas où elles sont rares et/ou onéreuses à rassembler. En cas de grande abondance de données, les résultats sont asymptotiquement les mêmes dans chaque méthode, la bayésienne étant simplement plus coûteuse en calcul. En revanche, la bayésienne permet de traiter des cas où la statistique ne disposerait pas d'assez de données pour qu'on puisse en appliquer les théorèmes limites.
Le psi-test bayésien (qui est utilisé pour déterminer la plausibilité d'une distribution par rapport à des observations) est asymptotiquement convergent avec le χ² des statistiques classiques à mesure que le nombre d'observations devient grand. Le choix apparemment arbitraire d'une distance euclidienne dans le χ² est ainsi parfaitement justifié a posteriori par le raisonnement bayésien.
Exemples d'inférence bayésienne : d'où vient ce biscuit ?
Imaginons deux boîtes de biscuits.
- L'une, A, comporte 30 biscuits au chocolat et 10 ordinaires.
- L'autre, B, en comporte 20 de chaque.
On choisit les yeux fermés une boîte au hasard, puis dans cette boîte un biscuit au hasard. Il se trouve être au chocolat. De quelle boîte a-t-il le plus de chances d'être issu, et avec quelle probabilité ? Intuitivement, on se doute que la boîte A a plus de chances d'être la bonne, mais de combien ?
La réponse exacte est donnée par le théorème de Bayes :
Notons HA la proposition " le gâteau vient de la boîte A " et HB la proposition " le gâteau vient de la boîte B ".
Si lorsqu'on a les yeux bandés les boîtes ne se distinguent que par leur nom, nous avons P(HA) = P(HB), et la somme fait 1, puisque nous avons bien choisi une boîte, soit une probabilité de 0,5. pour chaque proposition.
Notons D l'événement désigné par la phrase " le gâteau est au chocolat ". Connaissant le contenu des boîtes, nous savons que :
- P(D | HA) = 30/40 = 0,75
- P(D | HB) = 20/40 = 0,5.
Note: " P(A | B) " se dit " la probabilité de A sachant B ".
Résolution utilisant la notation des probabilités
La formule de Bayes nous donne donc :
Avant de regarder le gâteau, notre probabilité d'avoir choisi la boîte A était P(HA), soit 0,5.
Après l'avoir regardé, nous révisons cette probabilité à P(HA|D), qui est 0,6.