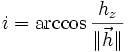Inclinaison - Définition
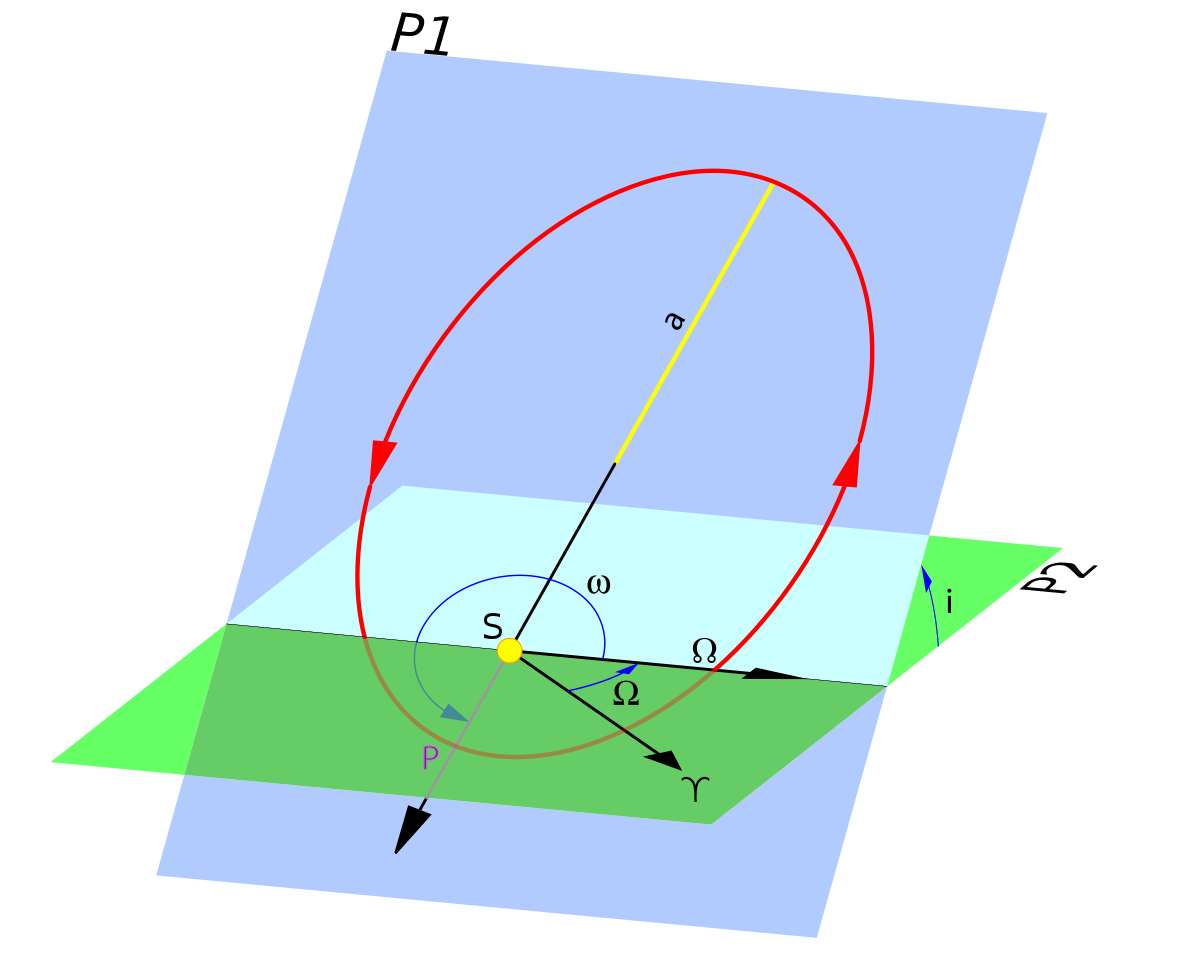
En mécanique céleste, l'inclinaison est un élément orbital d'un corps en orbite autour d'un autre. Il décrit l'angle entre le plan de l'orbite et le plan de référence (généralement le plan de l'écliptique, c'est-à-dire le plan moyen de l'orbite de la Terre, ou le plan équatorial). L'inclinaison est couramment notée par la lettre i.
Exemples
Dans le système solaire, l'inclinaison de l'orbite d'un corps céleste orbitant autour du Soleil (planètes, astéroïdes, etc.) est définie comme l'angle entre son plan orbital et celui de l'écliptique. Elle pourrait être mesurée par rapport à un autre plan, comme par exemple le plan équatorial du Soleil ou le plan orbital de Jupiter, mais le plan de l'écliptique est le plus pratique pour des observateurs terrestres. La plupart des orbites des corps du système solaire possédent une faible inclinaison, que ce soit par rapport à l'écliptique ou au plan équatorial solaire. Parmi les exceptions notables, on trouve les planètes naines Pluton (17°) et Éris (44°) et l'astéroïde (2) Pallas (34°).
Pour un satellite naturel ou artificiel, l'inclinaison est mesurée relativement au plan équatorial autour duquel l'objet orbite, s'il en est assez proche (le plan équatorial étant le plan perpendiculaire à l'axe de rotation du corps central). Dans ce cas :
- Une inclinaison de 0° signifie que l'objet orbite dans le plan équatorial et dans la même direction que la rotation du corps central ;
- Une inclinaison de 90° signifie que l'objet est sur une orbite polaire et passe au zénith des pôles nord et sud du corps central ;
- Une inclinaison supérieure à 90° signifie que l'objet orbite de façon rétrograde. Si elle est égale à 180°, il est situé sur une orbite équatoriale rétrograde.
Pour les objets situés loin du corps central, il est possible d'utiliser le plan de Laplace. Celui-ci est confondu avec le plan équatorial près du corps central et s'incline progressivement avec la distance pour finir par se confondre avec le plan orbital.
Si la rotation du corps central n'est pas connue avec précision, l'inclinaison d'un satellite sera donnée par rapport à l'écliptique ou parfois par rapport au plan de la sphère céleste (ou, de façon équivalente, comme l'angle entre l'axe de l'orbite et la direction de l'observateur). Cette dernière mesure est utilisée pour les objets externes au système solaire, comme les étoiles doubles. Elle dépend donc de la direction dans laquelle regarde l'observateur, c'est à dire de la région de la sphère céleste dans laquelle est situé l'objet. Les étoiles doubles possédant une inclinaison proche de 90° sont souvent des binaire à éclipses.
Dans le cas de la Lune, mesurer l'inclinaison par rapport au plan équatorial de la Terre conduit à une valeur variant rapidement (entre 18,29° et 28,58°). Il est plus utile de la mesurer par rapport à l'écliptique, ce qui donne une valeur relativement constante (5,145°).
Calcul
En astrodynamique, l'inclinaison i peut être calculée de la manière suivante :
où :
-
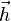
- hz est la composante sur z de ce vecteur.