Qubit - Définition

On nomme qubit (quantum + bit ; prononcé /kyoobit/), parfois écrit qbit, l'état quantique qui représente la plus petite unité de stockage d'information quantique. Il se compose d'une superposition de deux états de base, par convention nommés |0> et |1> (prononcés : ket 0 et ket 1). Un état qubit est constitué d'une superposition quantique linéaire de ces deux états. Une mémoire à qubits diffère significativement d'une mémoire classique :

Un bit classique se trouve toujours soit dans l'état 0, soit dans l'état 1. Un qubit peut quant à lui être soit dans l'état 0, soit dans l'état 1, soit dans une superposition de 0 et 1. Mais ce n'est pas un troisième état, c'est une infinité d'autres états. En général, le qubit est dans l'état , les coefficients étant des nombres complexes vérifiant | α | ² + | β | ² = 1. En fait, on peut postuler arbitrairement que α est un nombre réel positif, car multiplier un état par un nombre complexe de module 1 donne le même état.

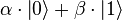
Lors de la mesure de la valeur du qubit, les seuls réponses pouvant êtres obtenues sont 0 ou 1. La probabilité de mesurer l'état 0 vaut | α | ², tandis que celle de mesurer l'état 1 vaut | β | ². Après mesure, le qubit se trouve dans l'état mesuré.

Une autre particularité du qbit par rapport à un bit classique est qu'il ne peut être dupliqué. En effet, pour le dupliquer, il faudrait pouvoir mesurer α et β d'un qbit (tout en préservant l'état du qbit), de sorte à préparer un autre qbit dans le même état . Ceci est doublement impossible : 1) Il est impossible de lire un qbit sans détruire définitivement son état (puisque après mesure le qbit est dans l'état mesuré). 2) Une mesure d'un qbit ne donne (et ne peux donner) aucune information sur α et β puisque le résultat est soit soit ce qui équivaut à (α,β) = (1,0) ou (0,1), ce qui ne correspond pas aux valeurs initiales de α et β.

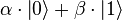
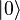
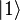
En revanche, il est possible de transporter l'état (la valeur) d'un qbit sur un autre qbit (le premier qbit est réinitialisé), par un processus de téléportation quantique. Mais ce processus ne donne aucune information sur α et β.

L'enjeu de l'informatique quantique est de concevoir des algorithmes, et les structures physiques pour les exécuter, tels que toutes les propriétés de la superposition soient utilisées pour le calcul, les qubits devant à la fin de l'exécution se trouver dans un état donnant le résultat de calcul sans risque d'obtenir un résultat aléatoire. On ne peut donc pas obtenir plus de données en autant de cycles qu'avec un ordinateur classique, mais on peut obtenir des résultats qui nécessiteraient plus de cycles. Pour la Science a par exemple expliqué qu'un algorithme quantique pouvait répondre à la question, à propos de deux cartes à jouer, "les deux cartes sont-elles de la même couleur", en autant de cycles qu'un algorithme classique en aurait besoin pour donner la couleur d'une seule des cartes. L'algorithme classique ne pouvait en revanche pas déterminer si les deux cartes étaient de la même couleur sans connaître les couleurs des deux cartes (attention, à la fin de l'exécution de l'algorithme quantique, on ne connait pas les couleurs, on sait juste si elles sont identiques ou non).

L'intérêt principal de l'ordinateur quantique serait que sa puissance est une fonction exponentielle au sens propre du nombre de qubits. En effet, si un qubit est dans une quelconque superposition d'états , deux qubits réunis sont quand à eux dans une superposition d'états , avec | α | ² + | β | ² + | γ | ² + | δ | ² = 1. Il s'agit cette fois d'employer la superposition des quatre états pour le calcul. Avec 10 qubits, on a 1024 états superposables, et avec n qubits, 2ⁿ. Donc, quand un opérateur est appliqué à l'ensemble des qubits, il est appliqué à 2ⁿ états en même temps, ce qui équivaut à un calcul parallèle sur 2ⁿ données en même temps. C'est pourquoi la puissance de calcul théorique d'un ordinateur quantique double à chaque fois qu'on lui adjoint un qubit.

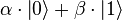
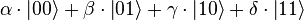
Le Commissariat à l'énergie atomique a réalisé un élément de circuit quantique baptisé quantronium. (lien). Une vue d'artiste symbolisant l'état de superposition a été réalisée pour illustrer l'annonce. (lien)