9 (nombre) - Définition

Introduction

9 (neuf) est l'entier naturel suivant 8 et précédant 10.

Dans le système international d'unités, le préfixe d'ordre de grandeur n'est plus défini pour 1000ⁿ quand n ≥ 9.

Évolution du glyphe

Au départ, divers Indiens écrivaient 9 d'une manière qui ressemble beaucoup au point d'interrogation, mais sans le point de la base. Les Kshtrapa, Andhra et Gupta commencèrent à incurver la ligne verticale du bas pour en faire un caractère ressemblant à notre 3. Les Nagari continuèrent le trait inférieur pour faire un cercle entourant cette sorte de 3, de la même manière pour l'arobase (qui encercle un minuscule a). Au cours du temps, le cercle qui entoure devint plus grand et sa ligne continua en dessous du cercle, et la sorte de 3 devint plus petit. Puis, tout cela rendit la sorte de 3 aussi petit qu'un trait. Les Arabes connectèrent simplement ce trait au milieu de la ligne descendante, et tout ce que les Européens ajoutèrent furent des fioritures.

En mathématiques

Neuf est un nombre impair et un nombre composé, ses diviseurs propres sont 1 et 3. C'est un carré parfait, le quatrième nombre puissant et un nombre cubique centré.

En base 10, un nombre est divisible par neuf si et seulement si la somme de ses chiffres est divisible par 9. Ainsi, pour déterminer si un nombre est divisible par 9 on peut le remplacer par la somme de ses chiffres, et ainsi de suite jusqu'à obtenir un nombre d'un seul chiffre; si ce chiffre est 9 (ou 0), le nombre initial est divisible par 9. Le seul autre nombre avec cette propriété est 3. En base N, les diviseurs de ont cette propriété. Une autre conséquence du fait que 9 = 10 − 1, fait que c'est aussi un nombre de Kaprekar. 9 est un nombre de Motzkin.

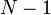
Six neuf consécutifs apparaissent dans les décimales de de la place 762 à la place 767. Ceci est connu comme le point de Feynman (voir aussi MathWorld).

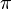
Il est un nombre pyramidal hexagonal.

En système de numération

Graphies actuelles

La graphie « 9 » n'est pas la seule utilisée dans le monde ; un certain nombre d'alphabets — particulièrement ceux des langues du sous-continent indien et du sud-est asiatique — utilisent des graphies différentes.