Algèbre linéaire - Définition

Quelques théorèmes

• Tout espace vectoriel de dimension finie possède au moins une base.
• Toutes les bases du même espace vectoriel de dimension finie ont un même nombre de vecteurs.
• Théorème de la « base incomplète » : soit E un espace vectoriel de dimension finie, G une famille génératrice de E et L une famille libre de vecteurs de G. Alors il existe au moins une base B de E telle que L soit incluse dans B et B incluse dans G.
• Tout espace vectoriel A possède un espace dual A^*; si A est de dimension finie, A^* est de même dimension.
• Formule de Grassmann : Soient E et G deux sous espaces vectoriels d'un même espace vectoriel de dimension finie. On a alors :

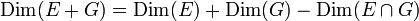
D'autres théorèmes concernent les conditions d'inversion de matrices de divers types :

• matrice diagonale
• bande
• matrice triangulaire
• à diagonale dominante (très utilisées en analyse numérique)

Un théorème intéressant à l'époque des mémoires d'ordinateurs de petite taille était qu'on pouvait travailler séparément sur des sous-ensembles (« blocs ») d'une matrice en les combinant ensuite par les mêmes règles qu'on utilise pour combiner des scalaires dans les matrices. Avec les mémoires actuelles de plusieurs gigaoctets, cette question a perdu un peu de son intérêt pratique, mais reste très prisée en théorie des nombres, pour la décomposition en produit de facteurs premiers avec le crible général de corps de nombres (GNFS) (méthode Lanczos par blocs).