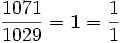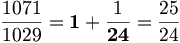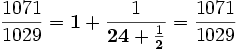Algorithme d'Euclide - Définition

Le théorème de Lamé

Le théorème de Lamé stipule que le nombre d'étape de l'algorithme d'Euclide exécuté sur deux entiers est borné (supérieurement) par cinq fois le nombre de chiffres nécessaire à écrire (en base 10) le plus petit de ces deux entiers.

On peut en fait être légèrement plus précis : le nombre d'étapes de l'algorithme d'Euclide exécuté sur deux entiers a et b, avec , est borné par la partie entière de , où ln désigne le logarithme naturel et est le nombre d'or.

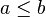
Comme le nombre de chiffres de l'écriture de b en base 10 est ln(b) / ln(10) et que la quantité est inférieure à 5 (elle vaut environ 4,78497), on retrouve bien le théorème de Lamé.

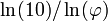
De plus, cette borne supérieure est la meilleure possible, puisqu'elle est atteinte quand a et b sont deux nombres de Fibonacci consécutifs.

Démonstration de sa finitude et de son exactitude

La définition même de la suite (a_n) par division euclidienne montre que, pour tout n tel que a_{n + 1} est non nul, il existe un entier q_{n + 2} tel que :

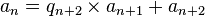
avec de plus . La suite d'entiers naturels (a_n) est donc strictement décroissante, et donc vaut 0 à un certain rang. L'existence d'un dernier reste non nul est ainsi établie.

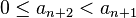
Soit N + 1 l'indice de ce dernier reste non nul. Il faut montrer que a_{N + 1} est bien le PGCD cherché. La relation précédente s'écrit donc ici , qui montre que a_{N + 1} divise a_N. Écrivant ensuite , on en déduit que a_{N + 1} divise aussi a_{N − 1} ; puis, de même, et par récurrence, que a_{N + 1} divise tous les termes de la suite a_n ; en particulier les premiers termes a et b. a_{N + 1} est donc bien un diviseur commun de a et b. Réciproquement, tout diviseur commun de a et b divisera aussi , et à nouveau par récurrence, divisera tous les termes de la suite (a_n) ; donc en particulier a_{N + 1}.

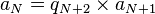
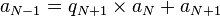
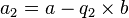
a_{N + 1} est donc un diviseur commun de a et b que divise tout autre diviseur commun ; c'est bien le PGCD.

Fractions continues

Les quotients successifs qui apparaissent quand l'algorithme d'Euclide est appliqué aux données a et b, sont précisément les nombres qui apparaissent dans la représentation sous forme de fraction continue de a/b. Considérons l'exemple de a = 1071 et b = 1029 utilisé ci-dessus.

Voici le calcul avec les quotients soulignés (successivement 1, 24 et 2):

1071 = 1029 × 1 + 42

1029 = 42 × 24 + 21

42 = 21 × 2 + 0

De cela on tire :

.

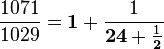
Dans l'égalité précédente, le second membre s'appelle la fraction continue ou continuée du quotient 1071/1029.

On peut en déduire les 3 approximations suivantes de la fraction, classées par ordre de précision croissante :

Cette méthode peut également être utilisée pour des nombres réels a et b  ;  comme dans le cas de deux entiers, la suite de quotients calculés représente la « décomposition en fraction continue » de a/b et fournit une suite d'approximations successives, de qualité croissante, du quotient a/b. Dans le cas où ce quotient est irrationnel, l'algorithme d'Euclide ne se termine pas et la suite des approximations obtenues est donc elle-même infinie !

nota : La décomposition en fraction continuée (et la série d'approximations successives correspondante) peut être appliquée, non seulement à un nombre réel quelconque, mais également à une fonction : cette démarche consiste à rechercher les approximants de Padé, dont on peut définir le principe comme suit : Au voisinage d'un point, le développement en série de Taylor d'une fonction donnée fournit un polynôme qui réalise une approximation de la fonction. Mais on peut également chercher une fraction rationnelle qui satisfasse les mêmes conditions que la partie polynômiale du développement de Taylor : l'égalité des dérivées de la fonction et de son approximation, jusqu'à un certain ordre donné.

La comparaison de ces deux types de développements permet de très intéressants développements (voir par exemple la démonstration de l'irrationalité de ζ(3)).