Analyse spectrale - Définition

Introduction

En physique et dans diverses techniques apparaissent des signaux, fonctions du temps ou, plus exceptionnellement, d'une variable d'espace. L'analyse spectrale recouvre plusieurs techniques de description de ces signaux dans le domaine des fréquences. Elle permet en particulier d'obtenir les caractéristiques de la réponse d'un système linéaire en utilisant une fonction de transfert. En mathématiques, l'analyse harmonique correspond à une partie de ces techniques.

Présentation

Un phénomène physique dépendant du temps est décrit par un ou plusieurs signaux. On ne peut qu'exceptionnellement les interpréter de façon simple. Le problème est de trouver une description de leur contenu, relativement générale et adaptée aux problèmes concrets. Ceux-ci se présentent souvent de la manière suivante : un système transforme un signal d'entrée en un signal de sortie, comment déterminer les caractéristiques de celui-ci en fonctions de celles du signal d'entrée et de celles du système ?

Dans le cas général, on ne connaît malheureusement pas la relation entre les valeurs du signal de sortie et celles du signal d'entrée mais seulement la relation entre les variations du signal de sortie et les valeurs (ou éventuellement les variations) du signal d'entrée. En termes mathématiques, le système est régi par une équation différentielle. Si celle-ci est quelconque, le problème est insoluble.

Heureusement, il existe une classe importante de systèmes, les systèmes linéaires (ou supposés tels) régis par le principe de superposition. Dans ce cas, correspondant à une équation différentielle linéaire, on peut essayer de décomposer le signal d'entrée en une somme de signaux simples auxquels on saurait faire correspondre des signaux de sortie également simples dont la somme donnerait le résultat cherché.

Le problème se simplifie encore plus si les caractéristiques du système restent constantes au cours du temps. On a affaire à une équation différentielle linéaire à coefficients constants. Les signaux simples sont les sinusoïdes qui subissent uniquement une amplification et un déphasage. C'est le problème de l'analyse spectrale : décomposer un signal compliqué en une somme de sinusoïdes.

Ici apparaît une difficulté car cette décomposition exige que le signal soit défini sur un temps infini. Or il ne peut être connu qu'à travers un enregistrement de durée limitée : il faut donc construire un modèle du signal en faisant des hypothèses, souvent évidentes intuitivement, sur la partie non enregistrée du phénomène.

Signaux périodiques

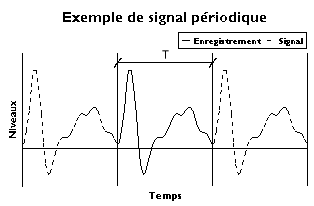
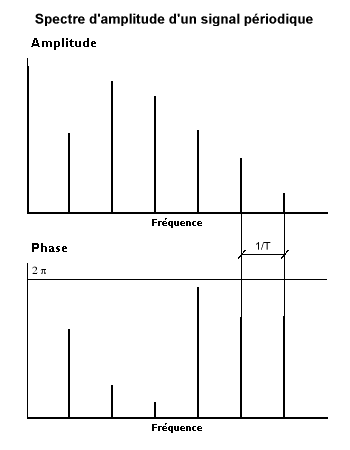
Le développement en série de Fourier d'un enregistrement de durée T associe à celui-ci des sinusoïdes d'amplitudes finies et de fréquences multiples de la fréquence du fondamental 1/T. On parle d'un spectre d'amplitude qui est un spectre de raies. Dans le cas général, le résultat de l'analyse peut s'exprimer soit en amplitudes et phases, soit en composantes cosinus et sinus.

La sommation des sinusoïdes crée un signal périodique. Si le signal d'origine est périodique, il est parfaitement représenté – au moins en principe. Dans le cas contraire on n'a représenté que l'enregistrement et il faut tenter de trouver autre chose.

Différents modèles

On peut supposer, par exemple, que le signal reproduit indéfiniment le contenu de l'enregistrement : on construit alors un modèle périodique basé sur la série de Fourier. Le signal est décrit par un spectre discret (ensemble de fréquences en progression arithmétique).

On peut aussi supposer que le niveau du signal est négligeable en dehors de l'enregistrement : on utilise dans ce cas un modèle transitoire basé sur la transformation de Fourier qui conduit en général à un spectre continu.

Il existe un certain nombre de phénomènes naturels pour lesquels aucune de ces deux hypothèses n'est réaliste. Par exemple, un enregistrement de vagues, sans montrer de périodicité, ne montre pas non plus de décroissance nette au cours de sa durée relativement faible : on parle alors de signal à variance finie (certains préfèrent parler de puissance finie mais ce n'est pas toujours pertinent techniquement), ce qui conduit à la notion de densité spectrale. On peut alors utiliser une hypothèse un peu plus floue selon laquelle la moyenne quadratique calculée sur l'enregistrement fournit une estimation raisonnable de la moyenne quadratique du signal. Ce type d'analyse conduit encore à un spectre continu. Il se définit, comme les précédents, à partir du signal mais on peut obtenir des informations supplémentaires en considérant celui-ci comme une réalisation d'un processus aléatoire.