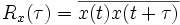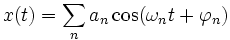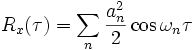Analyse spectrale - Définition

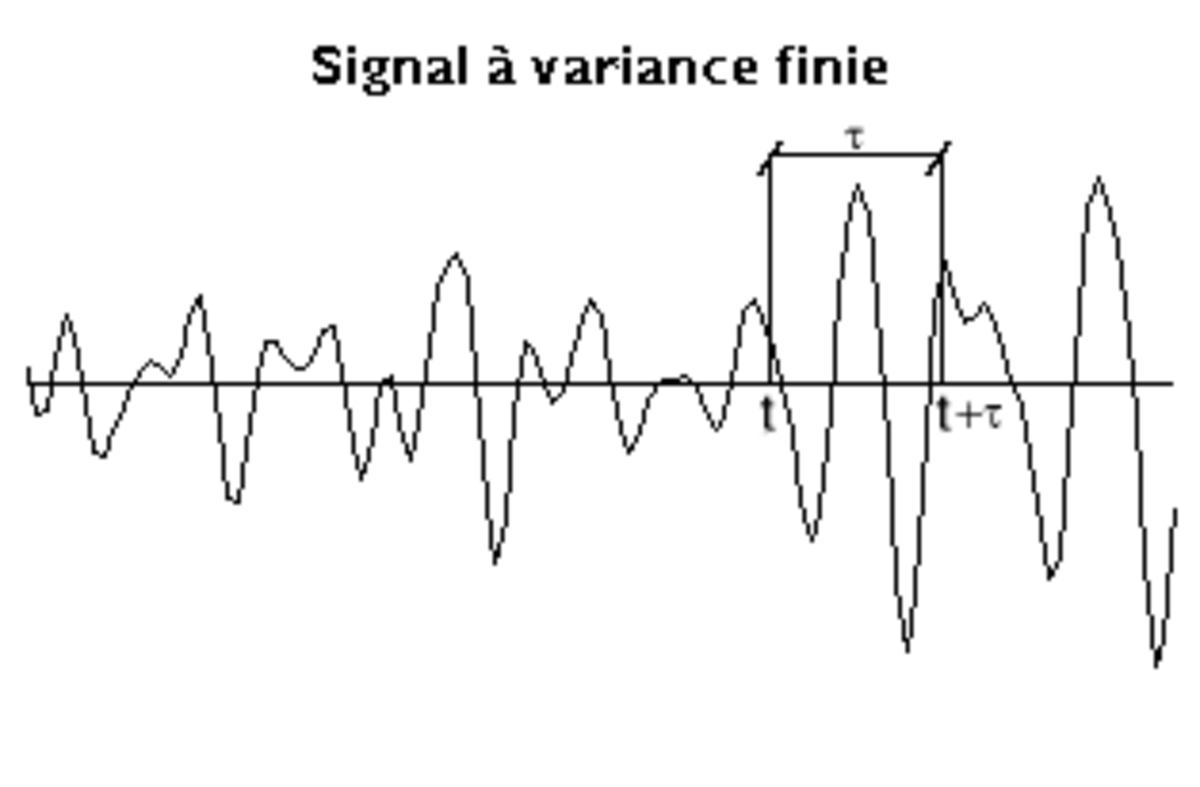
Signaux à variance finie

Le problème est plus compliqué que dans le cas précédent et on peut l'aborder de diverses manières. Celle que nous utiliserons n'est certainement pas la plus efficace d'un point de vue scientifique mais elle a l'avantage de montrer quelques points essentiels sans les cacher derrière des considérations mathématiques, sinon particulièrement difficiles, du moins assez lourdes. Pour s'affranchir de problèmes spécifiques liés à la prise en compte d'une moyenne non nulle, on supposera que le signal a été préalablement centré par soustraction de sa moyenne.

Fonction d'autocovariance

Etant donné un signal x(t), on appelle fonction d'autocovariance — souvent assimilée à tort à l'autocorrélation — la fonction de τ qui donne la moyenne des produits des valeurs de x(t) à deux instants qui diffèrent de τ :

Dans le calcul de cette moyenne, t varie de -∞ à +∞. Si le signal est transitoire, la fonction est nulle ; s'il est périodique, elle est elle-même périodique. En se plaçant dans le cas d'un signal qui n'appartient de toute évidence à aucune des deux catégories, la fonction possède les propriétés suivantes :

• Le changement de τ en -τ n'apporte aucune modification : la fonction est paire.
• À l'origine, R_x(0) représente la variance qui est nécessairement positive.
• La symétrie impose qu'il s'agisse d'un extremum. En fait, il s'agit d'un maximum : si dans le calcul on remplace le décalage 0 par un petit décalage τ, à chaque franchissement du niveau 0, on remplace un petit produit positif par un petit produit négatif.
• En exceptant le cas du signal périodique, deux points séparés par un grand décalage τ ont peu de choses en commun : la fonction tend vers 0 lorsque ce décalage tend vers l'infini.
• Au total, la fonction a souvent une vague allure de sinusoïde amortie.
• On veut, si c'est possible, assimiler le signal à une somme de sinusoïdes. Supposons que ce soit le cas. Que les amplitudes soient finies ou infiniment petites, on peut écrire cette somme sous la forme :

Dans ces conditions on montre que

Ainsi

• La fonction d'autocovariance contient les mêmes fréquences que le signal.
• Les amplitudes ne sont pas identiques mais elles sont obtenues par élévation au carré et division par 2.
• Les phases ont entièrement disparu : l'autocovariance correspond non seulement au signal d'origine, mais aussi à tous ceux qui contiennent les mêmes composantes.

Densité spectrale

On peut déduire de ce qui précède :

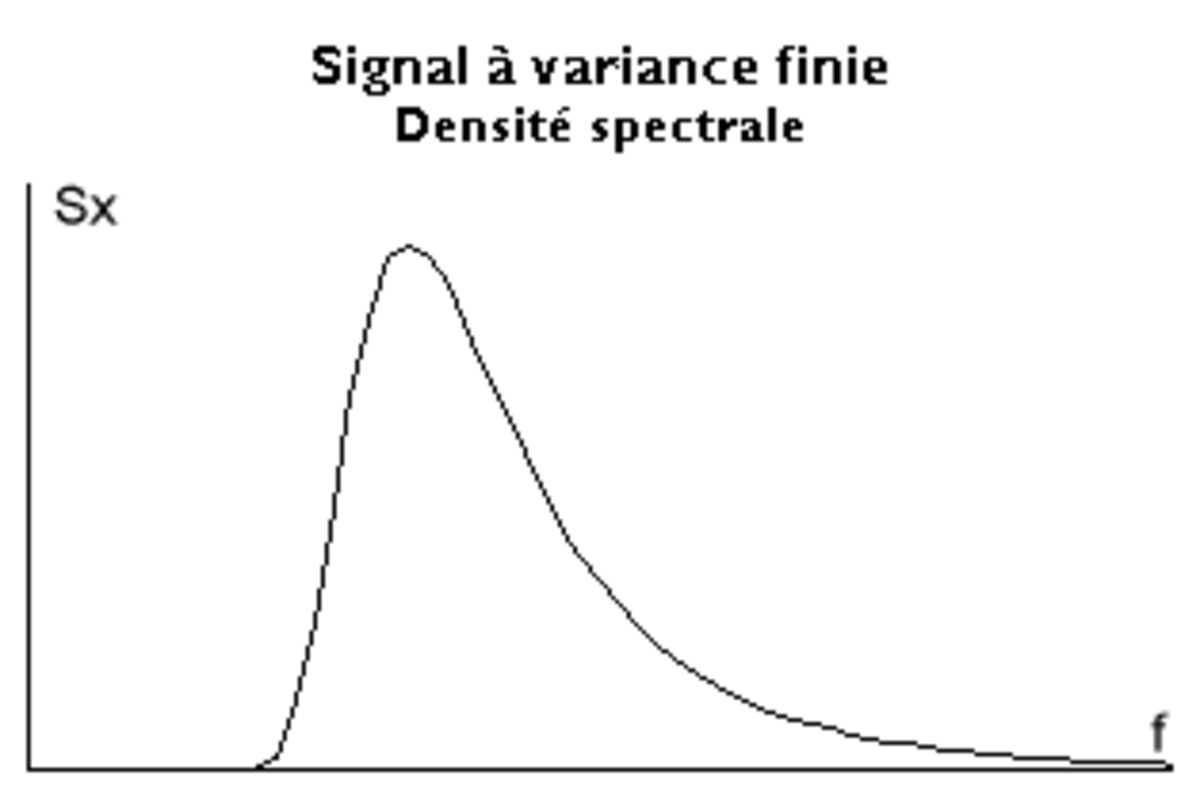
• La fonction d'autocovariance possède une transformée de Fourier que l'on nomme densité spectrale et que l'on note généralement S_x(f), f étant la fréquence.
• Les composantes de l'autocovariance étant homogènes à des carrés d'amplitude, la densité spectrale est non négative. Elle a une dimension (unité physique)² / Hertz.
• L'autocovariance étant une fonction réelle et paire, sa transformée de Fourier possède les mêmes caractéristiques.
• Un enregistrement tronquant toujours le signal censé se maintenir pendant un temps infini, la densité spectrale est nécessairement déformée par convolution.

Relation avec les processus aléatoires

À la déformation du contenu en fréquences déjà constatée pour les signaux transitoires s'ajoute une incertitude statistique liée à la position de l'enregistrement sur le signal.

La fonction d'autocovariance correspond à toute une famille de signaux qui contiennent les mêmes composantes. On peut interpréter cette famille comme celle des réalisations d'un processus continu. Un enregistrement de durée limitée peut également être considéré comme une réalisation d'un autre processus. Cela permet de préciser avec des intervalles de confiance la valeur statistique de l'analyse effectuée.