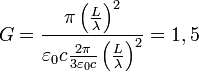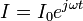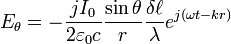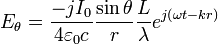Antenne dipolaire - Définition

Introduction

L'antenne dipolaire, élaborée par Heinrich Rudolph Hertz vers 1886, est une antenne constituée de deux brins métalliques, alimentée en son milieu et destinée à transmettre ou recevoir de l'énergie électromagnétique. Ce type d'antenne est le plus simple à étudier d'un point de vue analytique.

Dipôle élémentaire

Schéma géométrique d'un dipôle élémentaire.

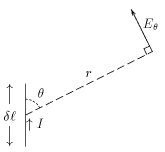
Un dipôle élémentaire est une petite longueur de conducteur (petite devant la longueur d'onde ) dans lequel circule un courant alternatif :

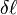
dans laquelle est la pulsation, et la fréquence.

est, comme d'habitude tel que  ; cette notation, employant des nombres complexes est la même utilisée quand on travaille avec le formalisme des impédances.

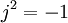
Il faut remarquer que ce type de dipôle ne peut être fabriqué pratiquement. Il faut bien que le courant vienne de quelque part et qu'il sorte quelque part. En réalité, ce petit morceau de conducteur et le courant qui y circule, sera simplement un des petits morceaux dans lesquels on divisera une antenne macroscopique, pour pouvoir la calculer.

L'intérêt est que l'on peut calculer facilement le champ électrique lointain de l'onde électromagnétique émise par ce petit bout de conducteur.

Si la distance de mesure du champ est beaucoup plus grand que la longueur d’onde, elle-même plus grande que la longueur du dipôle, nous donnons directement l’expression du champ électrique lointain (en V/m) :

où :

• ,
• est la constante de la permittivité du vide ;
• est la constante de la vitesse de la lumière dans le vide (en m/s) ;
• est la distance (en m) entre le dipôle et le point où le champ est evalué ;
• est la longueur (en m) du dipôle élémentaire ;
• est la longueur d’onde (en m) ;
• est le nombre d’onde (en rad/m) ;
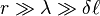
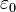
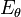
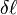
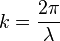
• l'exposant de rend compte de la variation de phase du champ électrique de l’onde avec le temps et avec la distance au dipôle.

Le champ électrique lointain de l'onde électromagnétique est coplanaire avec le conducteur ; il est aussi perpendiculaire à la ligne qui relie le point où il est évalué au conducteur (sauf sur la ligne du conducteur lui-même, où ce champ s’effondre totalement car y est nul), son orientation étant déterminée par celle du champ dans le conducteur et par le déphasage dépendant de la distance du point de mesure à ce conducteur.

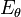
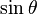
L'expression ne s’applique pas au champ électrique proche du conducteur dipôlaire (y compris celui au sein du conducteur lui-même).

Si nous imaginons le dipôle au centre d'une sphère et parallèle à l'axe nord-sud, le champ électrique de l'onde électromagnétique rayonnée sera parallèle aux méridiens et le champ magnétique de l'onde aura la même direction que les parallèles géographiques.

Si est la puissance de l'antenne dipôle, le champ électrique rayonné en un point situé à une distance de cette antenne, perpendiculairement à l'antenne (sens du vecteur de Poynting), est donné par la relation :

, avec en V/m, en W, en m.

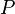
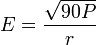
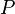
Ainsi, une source de 10 W produira un champ de 1 mV/m à une distance de 30 km, ce qui, en radioélectricité, n’est pas un champ négligeable.

Dipôle court

Courbe triangulaire du courant circulant dans une courte antenne dipolaire à deux brins horizontaux (de longueur totale L), alimentés en son centre par deux brins rapprochés (mais isolés) dans lesquels les courants entrant et sortant circulent en sens opposés.

Vue en perspective du rayonnement du dipôle élémentaire (vertical et invisible ici, au centre du tore montré posé sur le plan horizontal).

Le rayonnement du dipôle élémentaire, vu en coupe le long du dipôle, forme deux cercles jointifs au centre du dipole, et le champ électrique est orienté tangenciellement le long de ces cercles.

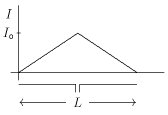
Un dipôle court est un dipôle réalisable pratiquement formé par deux conducteurs de longueur totale très petite comparée à la longueur d'onde . Les deux conducteurs sont alimentés au centre du dipôle (voir dessin de gauche).

Les brins parallèles rapprochés qui alimentent le dipôle en son centre sont traversés par des courants circulant en direction opposée, dont les champs électriques s'annulent mutuellement à distance suffisamment grande grande par rapport à leur distance mutuelle (supposée ici nulle). On peut alors les ignorer.

Le courant circule dans le même sens dans les deux bras du dipôle : vers la droite sur les deux ou vers la gauche sur les deux. On prend comme hypothèse que le courant est maximum au milieu du dipôle (là ou il est alimenté) et qu'il décroît linéairement jusqu'à zéro aux extrémités du dipôle où se concentrent les charges électriques déplacées par le courant alternatif.

Le champ lointain de l’onde électromagnétique rayonnée par ce dipôle est alors :

L'émission est maximale dans le plan perpendiculaire au dipôle et passant par son centre, mais décroit de façon inversement proportionnellement à la distance. Elle est nulle dans la direction des conducteurs qui est la même que la direction du courant.

Le diagramme d'émission a la forme d'un tore de section circulaire et de rayon interne nul. Dans les deux images de droite, le dipôle ferme deux courts segment verticaux jointifs au point d'alimentation des deux brins, qui se trouve donc au centre du tore posé sur un plan horizontal.

À partir de ce champ électrique on peut calculer la puissance totale émise par ce dipôle et à partir de ça, calculer la partie résistive de l'impédance série de ce dipôle :

ohms pour

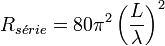
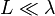
mais en revanche :

ohms pour

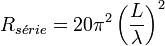
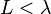
Le gain de cette antenne (obtenu en remplaçant dans l’expression générale du gain) est :

= 1,76 dBi