Axiomes de plans projectifs/Suite des axiomes - Définition

Transformations et configurations utiles

Configurations unidimensionnelles

Les 2 configurations unidimensionnelles élémentaires du plan projectif d'incidence (PPI) sont : la droite, ensemble de points alignés ainsi que le « faisceau », ensemble de droites concourantes en un point.

On pourra ensuite étudier le « faisceau de coniques », ensemble de coniques qui ont 4 points communs, etc.

Transformations de configurations unidimensionnelles

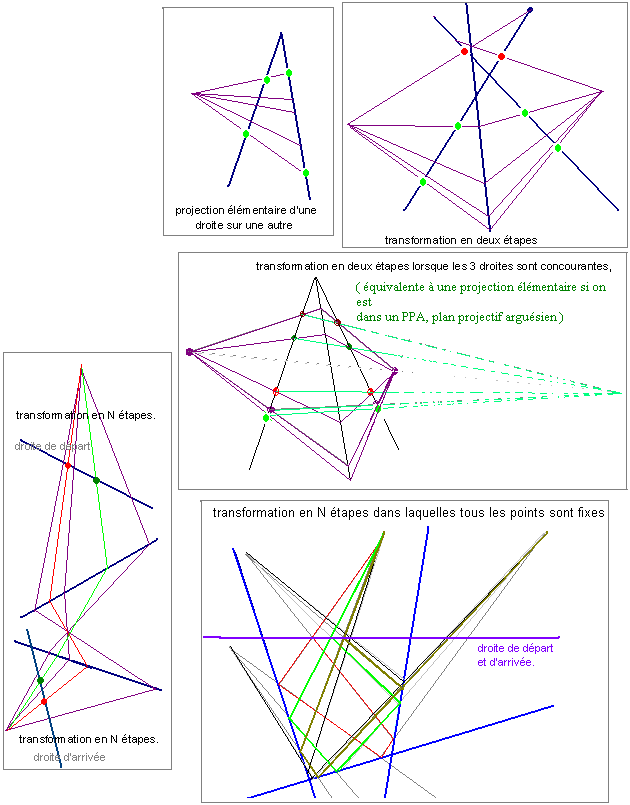
Dans le droit héritage de la perspective de la Renaissance il est intéressant d'étudier certaines transformations telles que les transformations d'un alignement de points en un autre alignement de points, que l'on appelle les transformations unidimensionnelles. Par exemple la projection élémentaire d'une droite sur une autre, la transformation en deux étapes, la transformation en deux étapes lorsque les 3 droites sont concourantes, la transformation en N étapes. Quels sont les invariants d'une telle transformation, quels axiomes sont indispensables ?

Transformation projective unidimensionnelle identité sur une droite

Lorsque l'on effectue une transformation unidimensionnelle en N étapes et que l'on revient sur la droite de départ, quelles sont les conditions pour que cette transformation laisse tous les points fixes ?

Transformations projectives bidimensionnelles

Sur un plan en dimension 2, on envisage aussi les transformations bidimensionnelles, celles qui transforment un point du plan en un autre point du plan. Parmi elles, celles qui conservent l'alignement des points ; conservent-elles aussi la convergence des droites ? Parmi elles, celles qui laissent fixes seulement les points d'une droite particulière, appelées dilatations. Comment ces différentes transformations se combinent-elles, leur loi de composition interne fait-elle apparaître des structures de monoïde, de groupe, le produit de 2 transformations est-il toujours commutatif ?

Quelques configurations utiles.

• Un bipoint projectif n'a rien à voir avec les vecteurs classiques, c'est simplement un ensemble non-ordonné de 2 points. Idem pour la bidroite.
• Un triangle est un ensemble non-ordonné de 3 points ; Un trigone ou tri-côté ou tri-latère est un ensemble non-ordonné de 3 droites. Triangle et trigone sont souvent confondus car ils sont duaux l'un de l'autre, cette tolérance de langage ne prête pas à conséquence.
• En revanche, un quadrangle complet est un ensemble non-ordonné de 4 points, il donne naissance à 6 côtés et 3 points diagonaux ; un quadrilatère complet est un ensemble non-ordonné de 4 droites, il donne naissance à 6 sommets et 3 droites diagonales.
• La même nuance est valable pour distinguer un hexagone d'un hexangle lorsqu'il y a un risque de confusion.

Questions soulevées par l'explosion combinatoire

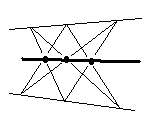
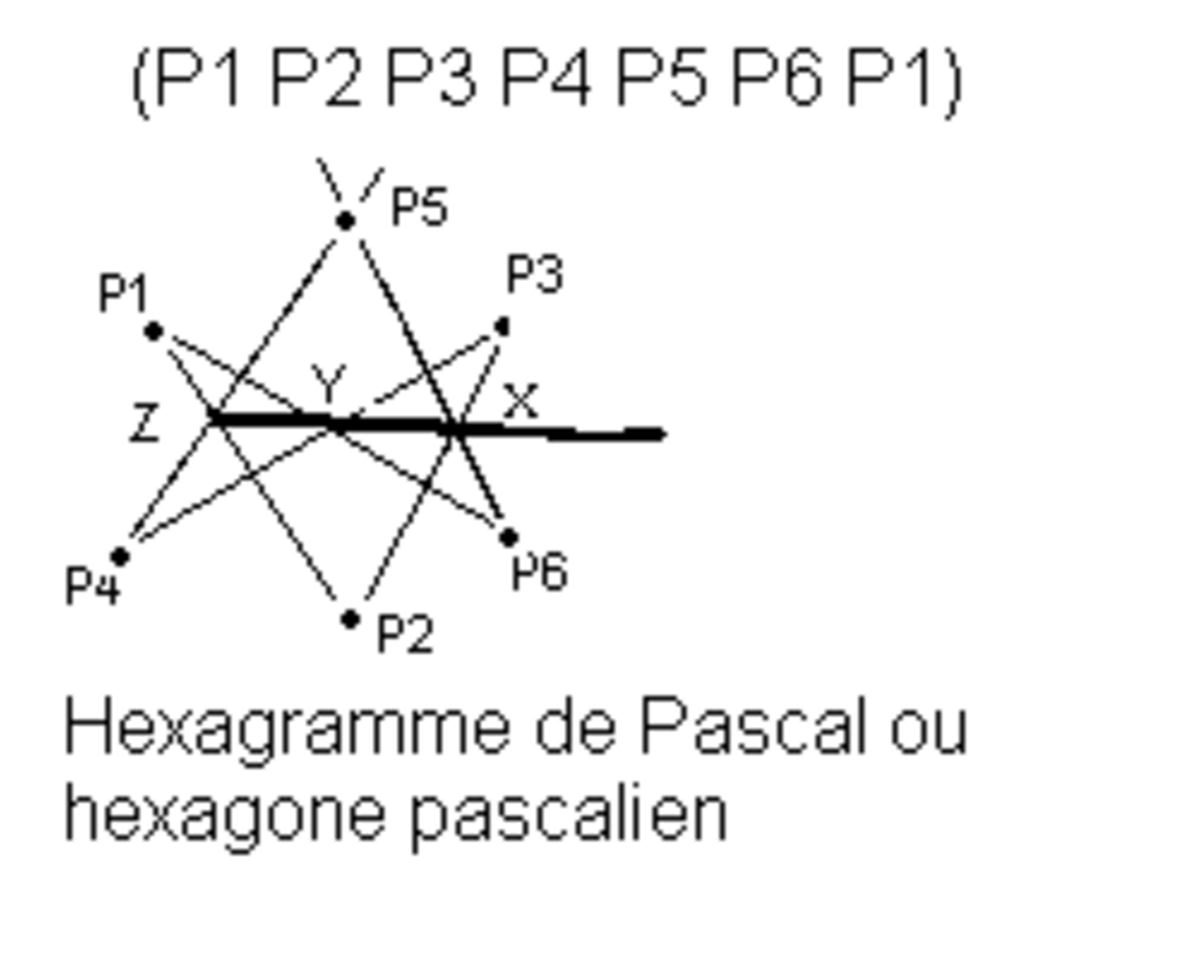
Si l'on observe la configuration de Désargues, on constate que 4 couples de triangles peuvent être créés. En plus de ABC-A'B'C' sur lequel on a coutume de travailler, il y a aussi ABC'-A'B'C, AB'C'-A'BC et AB'C-A'BC' qui donnent 3 nouvelles droites de Désargues, d'où un quadrilatère complet ; de plus, la même étude combinatoire menée sur le théorème dual conduit à 4 triangles qui donnent, outre le point O, 3 autres points de convergence des côtés, d'où un quadrangle complet. Quelles sont les propriétés de ce quadrangle et de ce quadrilatère, comment se déduisent-ils l'un de l'autre ? La configuration de Pappus offre une plus forte permutation ; il y a 6 hexagrammes non dégénérés (A1 C2 B1 A2 C1 B2, dessiné ci-contre ; A1 C2 B1 B2 C1 A2 ; A1 B2 B1 C2 C1 A2 ; A1 B2 B1 A2 C1 C2 ; A1 A2 B1 B2 C1 C2 ; A1 A2 B1 C2 C1 B2 ; ), donc 6 droites de Pappus. Quelles sont les propriétés de ces 6 droites ? En fait on peut démontrer qu'elles sont concourantes en deux groupes de 3. Mais de quels axiomes minimaux a-t-on besoin pour démontrer cette propriété ? L'axiome Fondamental de la géométrie projective est-il indispensable ? l'axiome de Désargues suffirait-il ? Quant à l'hexagramme de Pascal (voir Traité projectif des coniques), de nombreux mathématiciens du XIX^e siècle se sont penchés sur les diverses permutations du parcours des 6 points. Il s'agit particulièrement de Bauer, Catalan, Cayley, Fontaneau, Gräfe, Grossmann, Hesse, Jörres, Kirkman, Ladd-Franklin-Christine, Little  , Lüroth, Meyer, Molk, Plücker, Salmon, Jakob Steiner, Veronese-G., von Staudt. Avec 6 points, on peut réaliser 60 parcours hexagonaux, donc 60 droites de Pascal. Quelles sont les propriétés de ces 60 droites, comment sont disposées leurs intersections dans le plan ? Quel rapport avec les 60 points de Brianchon que l'on peut dualement envisager ? Par exemple Steiner a montré qu'elles sont concourantes 3 à 3, d'où 20 « points de Steiner ».