Axiomes de plans projectifs/Suite des axiomes - Définition
La liste des auteurs de cet article est disponible ici.
Cascade de théorèmes entre ces axiomes
Les diverses sortes de plans découlent les uns des autres comme des bassins de plus en plus larges reliés par des cascades.
___ ____ ____ ____ ____ ____ ____ / __) (____) (____) (____) (____) (____) (__ \ | | __________ | | | | \ PP bary-\ | | | | \centrique\ | | | | \==========\ | | | | ______________!__ | | |_ \ \ |_| |_| \PP homogène =====\\ |_| _ \________________\ \\ | | | | ______||_______ | | | | \ || \ | | |_| // ((____)) ) \ |_| |_| |||\PP fondamental \ |_| _ || \_______________\ | | | | || | | | | ____||__ ____________ | | | | \ || ) \ | | |_| // (____)) ) _\ |_| |_| |||\ PP de Pappus \ |_| _ || \____________________\ | | | | ____||___________________ | | | | \ || ) \ | | |_| \(____)) ) _\ |_| | | \ )) \ | | |_| \ PP de Désargues \ |_| _ \________________________\ | | | |__ ____ ____ ____ ____ ____ __| | \___) (____) (____) (____) (____) (____) (____/ Depuis l'incidence vers Pappus ?
Munis des seuls axiomes du PPI -plan projectif d'incidence- on ne peut pas démontrer l'alignement de trois points dans la configuration de Pappus.
En géométrie analytique
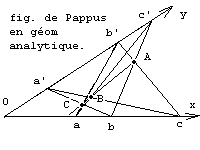
On pourrait démontrer ainsi le théorème de Pappus en géométrie analytique en coordonnées cartésiennes.
- Droite ab' : b'x+ay= ab'
droite ba' : a'x+by= a'b ; leur intersection C a pour coordonnées
-
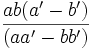
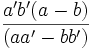
- De même A
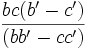
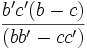
- Pour établir l'alignement, calculons d'abord les coordonnées du vecteur AC
![\frac{bb'[aa'(b-c)+bb'(c-a)+cc'(a-b)]}{(aa'-bb')(bb'-cc')}](https://static.techno-science.net/illustration/Definitions/autres/4/4c99a6a7d67d98a9b54bd94fcec03c74_ae4651ec91cd0feb979cc9ec5f5aaa54.png)
- et
![\frac{bb'[aa'(b'-c')+bb'(c'-a')+cc'(a'-b')]}{(aa'-bb')(bb'-cc')}](https://static.techno-science.net/illustration/Definitions/autres/5/5ebe989432927e531a4708832a4efea1_7e527e3e7b5242ca34a2071b5f2a1428.png)
- donc vecteur AC//vecteur [aa'(b − c) + bb'(c − a) + cc'(a − b)], [aa'(b' − c') + bb'(c' − a') + cc'(a' − b')]
- un calcul similaire donnera un vecteur colinéaire à BA
- [aa'(b − c) + bb'(c − a) + cc'(a − b)], [aa'(b' − c') + bb'(c' − a') + cc'(a' − b')], ces deux vecteurs BA et AC sont colinéaires et ont un point commun, donc ABC sont alignés.
- La vérification est établie. Les calculs sont valables dans un corps commutatif K (réels, complexes ou autres), mais on n'a pas fait le lien avec la géométrie. L'analytique cache les causes plus profondes.
![\frac{bb'[aa'(b-c)+bb'(c-a)+cc'(a-b)]}{(aa'-bb')(bb'-cc')}](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/4c99a6a7d67d98a9b54bd94fcec03c74_ae4651ec91cd0feb979cc9ec5f5aaa54.png)
![\frac{bb'[aa'(b'-c')+bb'(c'-a')+cc'(a'-b')]}{(aa'-bb')(bb'-cc')}](https://static.techno-science.net/illustrationWebp/Definitions/autres/5/5ebe989432927e531a4708832a4efea1_7e527e3e7b5242ca34a2071b5f2a1428.png)
Les birapports
Une démonstration possible du théorème de Pappus peut se faire en utilisant le birapport ou rapport anharmonique. Son exposé traditionnel nécessite les longueurs qui sortent de la géométrie projective stricte. En revanche, on peut définir le birapport sans aucun recours aux notions métriques.
Les homographies
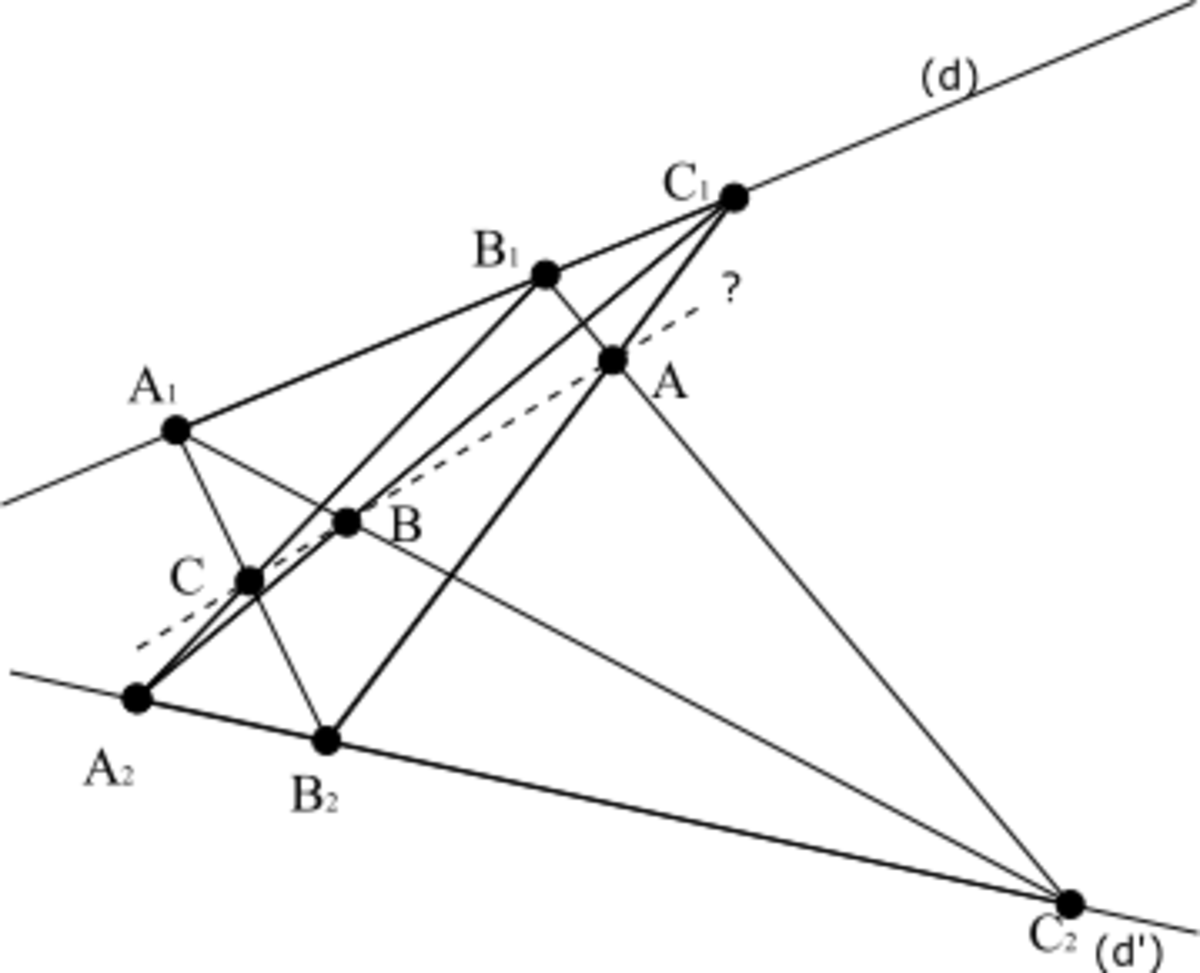
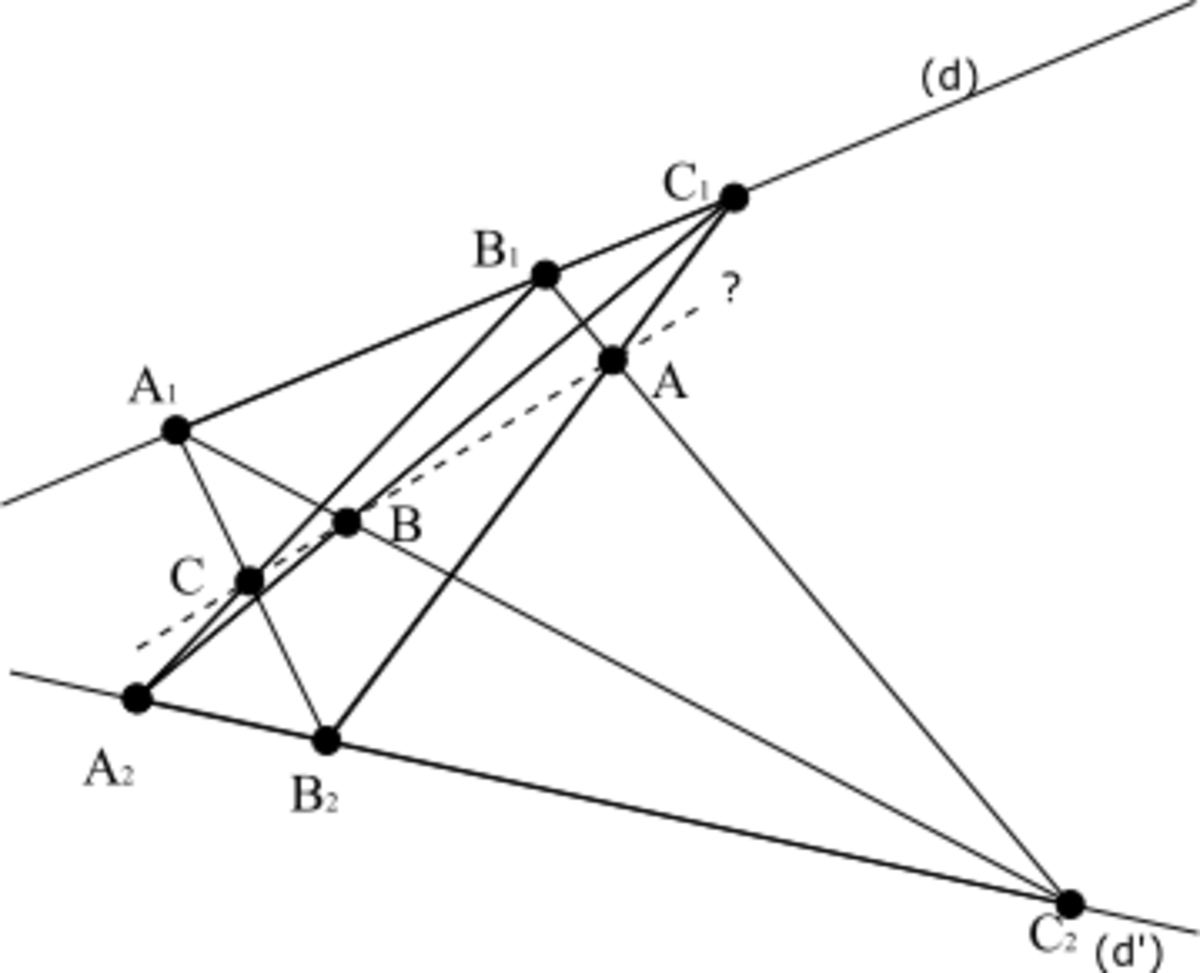
Il serait possible de faire appel aux transformations homographiques du plan qui sont très puissantes. Plus modestement on utilisera des transformations perspectives unidimensionnelles qui découlent d'un axiome fondamental de la géométrie projective.
Du plan fondamental vers Pappus
Ce théorème s'énonce ainsi :
- Un plan projectif fondamental (PPF) est pappusien (PPP).
Il se démontre en utilisant une transformation unidimensionnelle identité judicieusement choisie.
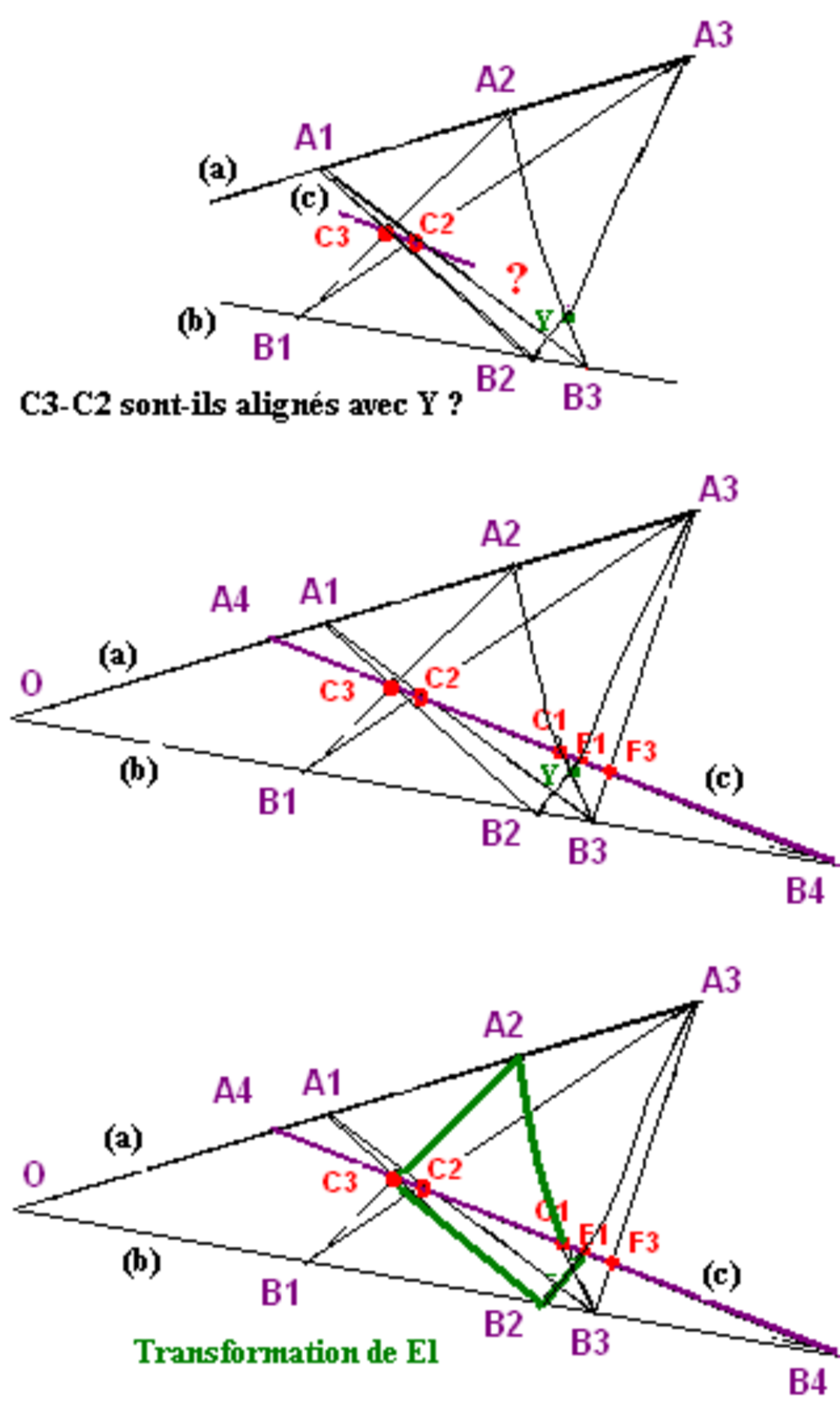
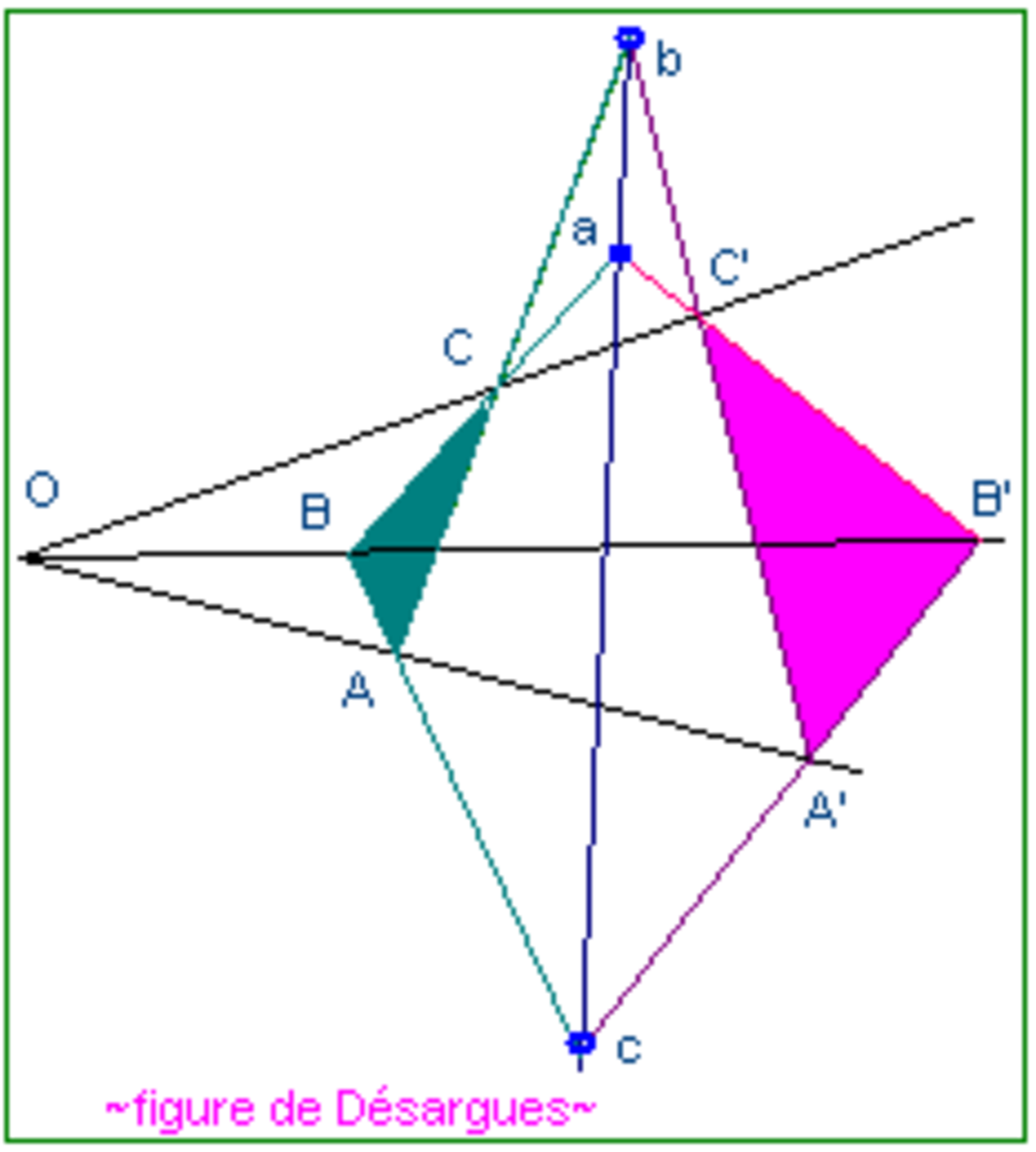
depuis Pappus vers Désargues
Il s'agit du Théorème d'Hessenberg version projective. Énoncé :
- Un plan projectif de Pappus (PPP) est arguésien (PPA).
Mais il existe des plans arguésiens qui ne sont pas pappusiens. Une démonstration possible, n'ayant pas besoin du théorème fondamental de la géométrie projective, nécessite la création de points d'intersections supplémentaires et l'emploi à trois reprises de l'axiome de Pappus.
On a les deux triangles ABC et A'B'C' en perspective depuis O. On définit des points auxiliaires : T=AC*A'C' ; U=AB*A'B' ; D=AB*OT ; E=DB'**A'C' ; F=EA*oC' ; V=EA*OB' ; les droites auxiliaires GAMMA=DF ; DELTA=TV et W=BC*GAMMA ; W'=B'C'*GAMMA. Le but est de montrer que : U est sur DELTA et W W' sont confondus.
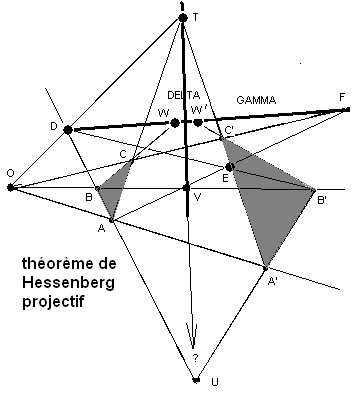
On applique l'axiome de Pappus aux alignements OAA' et EB'D ⇒ TVU alignés (sur DELTA par conséquent). On applique l'axiome de Pappus aux alignements OFC et ABD ⇒ TVW alignés (sur DELTA par conséquent). On applique l'axiome de Pappus aux alignements OFC' et EB'D ⇒ TVW' alignés (sur DELTA par conséquent). Il s'ensuit que W et W' sont à la fois sur DELTA et GAMMA, donc sont un point unique (un axiome des PPI). Donc TUW sont sur DELTA. Or on avait défini W sur BC et W' sur B'C', donc W=BC*B'C'. On a bien démontré le théorème de Désargues, les intersections respectives de AB, BC, CA avec A'B', B'C', C'A' sont alignées.
Du plan homogène vers le fondamental
Ce théorème s'énonce ainsi :
- Un plan projectif homogène (PPH) est fondamental (PPF).
Remarque : ce théorème utilise les propriétés algébriques du corps commutatif K.
On considère dans un PPhomogène une transformation projective unidimensionnelle d'une droite sur elle-même qui comporte trois points fixes. Est-elle l'identité projective unidimensionnelle ?
- Soient la droite (u ; v ; w), trois de ses points P1 = [ wD ; wE ; -(uD+vE) ], P2 = [ wL ; wM ; -(uL+vM) ], P3 = [ w (D + hL) ; w (E + hM) ; -(uD+vE) -h(uL+vM) ] et une transformation projective unidimensionnelle T de formule générale (cas où w est non-nul) :
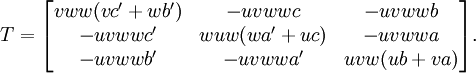
- L'expression que les trois points P1, 2 et 3 sont fixes conduit à trois équations dont les inconnues sont a b c a' b' c' :
- (uv2a + wu2c + uw2a') * DE − (u2vb + vw2b' + v2wc') * DE + (u2va − uvwc') * D2 − (uv2b − uvwc) * E2 = 0
- (uv2a + wu2c + uw2a') * LM − (u2vb + vw2b' + v2wc') * LM + (u2va − uvwc') * L2 − (uv2b − uvwc) * M2 = 0
- (uv2a + wu2c + uw2a') * (D + hL)(E + hM) − (u2vb + vw2b' + v2wc') * (D + hL)(E + hM) + (u2va − uvwc') * (D + hL)2 − (uv2b − uvwc) * (E + hM)2 = 0
- Qui conduisent dans une première étape, en posant pour des raisons d'homogénéïté deux nombres arbitraires k^3, g=1, à 4 nouvelles équations où les variables (D E L M h) des coordonnées des 3 points sont éliminées :
- (uv2a + wu2c + uw2a') = k3g = (u2vb + vw2b' + v2wc')
- (u2va − uvwc') = 0
- (uv2b − uvwc) = 0. Ce qui conduit à definir les paramètres c a' b' c' par
- wc = vb
- uw2a' = k3g − uv(va + ub)
- vb' = ua'
- wc' = ua
- La transformation qui conserve les trois points fixes sur la droite s'écrit alors :
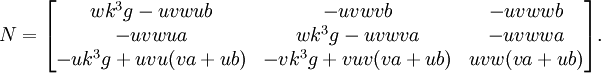
- Un point quelconque de la droite concernée est P = [ wX ; wY ; -(uX+vY) ] et on vérifie que N*P=w*k^3*g*P, tous les points de la droite sont donc fixes.
- Il s'agit de la transformation identité (N) sur cette droite ; par conséquent le plan homogène respecte l'axiome fondamental du plan projectif fondamental. Ainsi il est démontré qu'« un plan projectif homogène (PPH) est fondamental (PPF) ».
Remarque : après ce théorème démontré nécessairement par une méthode de géométrie analytique, quasiment toute la suite de l'étude de la géométrie projective pourra se faire sans calculs analytiques.
Depuis Désargues vers les coniques
Parvenus à ce point, on peut introduire les coniques. L'approche des coniques peut être fondée sur le théorème de Pascal. Plusieurs définitions des coniques peuvent être adoptées :
- en termes de courbes du second degré.
- en termes d'intersection d'un cône et d'un plan. C'était la définition bimillénaire, voir conique.
- en termes de faisceaux de droites en correspondance homographique.
- en termes de birapport constant.
- en termes de courbe autoduale, comme le fait H.S.M. Coxeter.
On peut adopter une discipline axiomatique.
