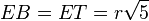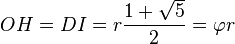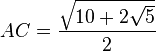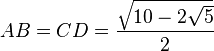Construction du pentagone régulier à la règle et au compas - Définition

Constructions contemporaines

Commentaires de l'animation

L'animation utilise la propriété suivante : dans le pentagone ABCDE ci-dessus, inscrit dans un cercle de rayon 1, on peut démontrer, en utilisant le théorème de Pythagore, que les côtés AC et AB ont pour longueurs respectives :

Commentaires de l'animation

En effet, AC est un côté de l'angle droit dans le triangle rectangle AA'C, dont les deux autres dimensions sont 2 et .

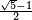
Quant à DC, la présence d'angles droits dans le quadrilatère ACA'D permet d'affirmer que AA' × DC = 2 × AC × A'C

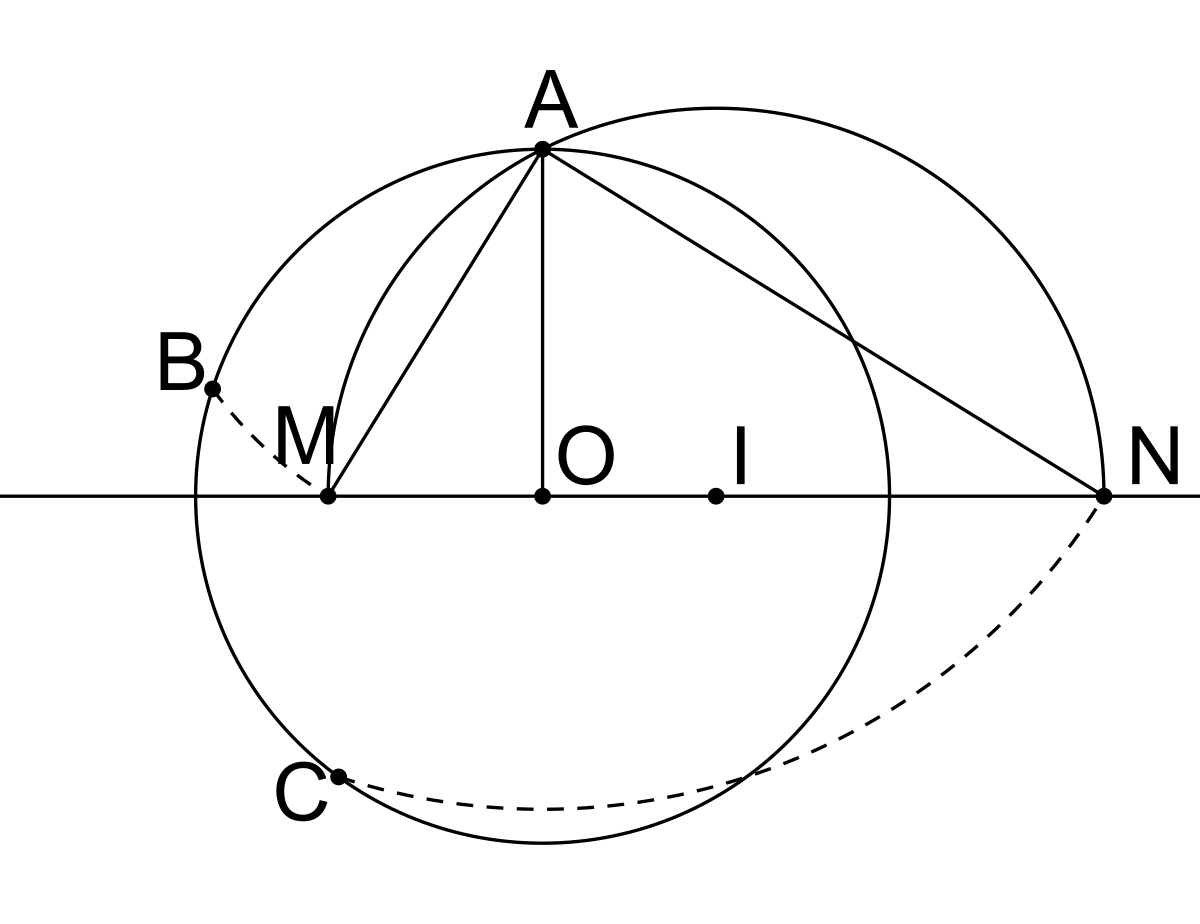
Dans l'animation présentée, les deux derniers cercles construits ont pour rayons AM et AN (voir figure ci-contre). Or AM est l'hypoténuse du triangle rectangle MOA dont les deux autres dimensions sont 1 et . donc le théorème de Pythagore permet de prouver que AM correspond bien à la longueur AB.

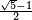
Quant à AN, c'est l'hypoténuse du triangle rectangle ONA dont les autres dimensions sont 1 et donc AN correspond bien à la longueur AC.

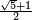
Pentagone inscrit dans un cercle

On peut grandement simplifier la construction d'Euclide en conservant le même principe : construire des triangles d'or ou d'argent.:

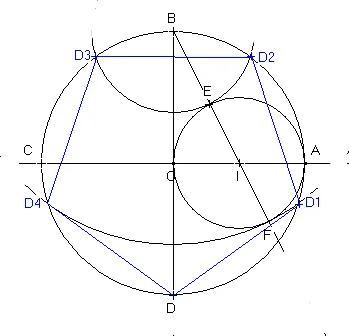
1. Tracer un cercle Γ de centre O et de rayon R (unité quelconque)
2. Tracer 2 diamètres perpendiculaires
   • les jonctions à Γ formant les point A, B, C, D
   • A étant diamétralement opposé à C
   • B étant diamétralement opposé à D
3. Tracer un cercle Γ ' de diamètre [OA] (rayon R' = R/2) et de centre I
   • Γ ' passe donc en O et A
4. Tracer une droite (d) passant par B et I
   • (d) intercepte Γ ' en E et F (E est le plus proche de B)
5. Tracer 2 (arc de) cercles Γ1 et Γ2 de centre B et de rayons (respectivement) BE et BF
   • Γ1 et Γ2 interceptent Γ en 4 pts (D1, D2, D3, D4)

D, D1, D2, D3, D4 forment un pentagone régulier

En effet, on vérifie que BOD2 est un triangle d'or, BOD1 un triangle d'argent (leurs bases valent respectivement et alors que leurs côtés valent R).

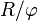
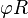
Pentagone dans un cercle dont le rayon n'est pas l'unité

1. On utilise un repère orthonormé (OIJ) (Constructible puisque l'on sait construire un angle droit et reporter une longueur!)
2. On place le point A(-1/2,0) et on trace le cercle bleu de centre A passant par J. Ce cercle coupe l'axe des abscisses en deux points, soit B le point d'abscisse positive
3. On trace le cercle vert de centre O passant par J
4. Soit C le milieu de [OB]. La parallèle à l'axe des ordonnées passant par C coupe le cercle vert en un point D.
5. Avec le compas on reporte successivement la longueur ID sur le cercle vert
6. On obtient ainsi le pentagone rouge

Démonstration :

Montrons que OC = cos(2π / 5)= .
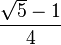
Le Théorème de Pythagore dans le triangle AOJ donne AJ² = (1/2)² + 1².
Or AB = AJ (rayons du cercle bleu) et OB = AB - AO. D'où OB = AJ -(1/2), soit OB = , d'où le résultat puisque OC = 1/2 OB.

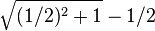
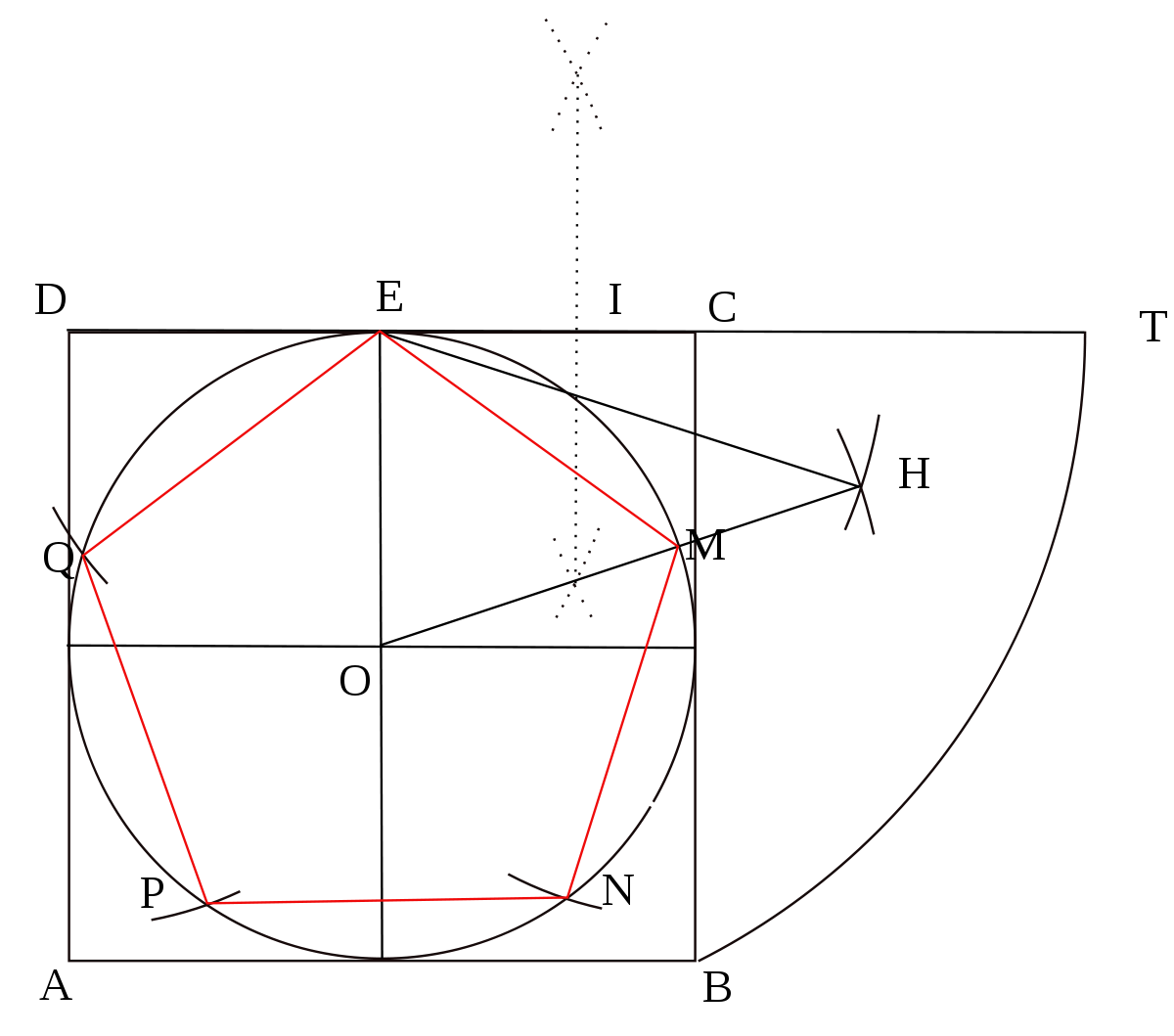
Pentagone inscrit dans un cercle inscrit dans un carré.

1. Tracer un carré ABCD. Placer E milieu de [CD].
2. Tracer le cercle Γ de centre O et de rayon OE inscrit dans ce carré.
3. Placer T le point de la demi-droite [DC) tel que: ET=EB.
4. Placer I le milieu de [DT].
5. Tracer le triangle OHE isocèle en H tel que: OH=DI. La droite (OH) coupe le cercle Γ en M.
6. La distance EM est la longueur des côtés du pentagone inscrit dans Γ .

Démonstration : Si on appelle r le rayon du cercle inscrit, on peut démontrer grâce au théorème de Pythagore que . D'où il vient que où est le nombre d'or. Le triangle OEH est alors un triangle d'or et l'angle EOM vaut donc 72° (angle au centre dans un pentagone régulier).