Courbe algébrique - Définition

Cas général

Régularité

Soit X une variété algébrique intègre de dimension 1. Alors les propriétés suivantes sont équivalentes

• X est normale (c'est-à-dire que pour tout ouvert affine U, l'anneau O_X(U) est intégralement clos);
• O_X(U) est un anneau de Dedekind pour tout ouvert affine U;
• l'anneau local O_X,x est un anneau de valuation discrète pour tout point fermé x;
• X est une variété algébrique régulière, c'est-à-dire que O_X,x est un anneau local régulier pour tout point x.

Si le corps de base k est parfait, ces propriétés sont équivalentes à

• X est non-singulière (ou lisse), c'est-dire que après extension du corps de base à la clôture algébrique de k, la variété est régulière.

Projectivité

Une courbe algébrique est projective si et seulement si elle est propre. Elle est propre si et seulement chaque composante irréductible est propre. Une courbe irréductible est propre si et seulement si elle n'est pas affine.

Ainsi une courbe algébrique intégre est soit affine, soit projective.

Courbes singulières ou non projectives

Si C est une courbe algébrique séparée, alors elle est quasi-projective. Si aucune de ses composantes irréductibles n'est projective, alors elle est affine.

Une courbe peut présenter des singularités, au si on prend sa normalisation C', alors est un morphisme fini surjectif, et C' est une courbe régulière.

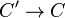
Courbes sur des corps particuliers

Sur les nombres complexes

Sur les corps globaux

Mordell-Weil, Mordell

Sur les corps finis

Comptage des points: hypothèse de Riemann sur un corps fini.