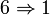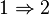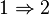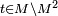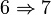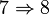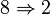Anneau de valuation discrète - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Définitions et exemples - Critères - Propriétés

Introduction

En mathématiques, plus précisément en algèbre commutative, un anneau de valuation discrète est un anneau de valuation dont la valuation est discrète mais non triviale. Un anneau est de valuation discrète lorsqu'il est principal, qu'il ne possède qu'un idéal maximal, et que cet idéal est non nul.

Cette notion est utilisée en théorie algébrique des nombres et en géométrie algébrique ; elle constitue un outil d'étude des anneaux noethériens, en particulier les anneaux de Dedekind.

Définitions et exemples

Définitions

La première définition est presque une lapalissade :

Première définition — Un anneau de valuation discrète est un anneau de valuation dont la valuation est discrète mais non triviale.

Autrement dit, A est un anneau commutatif unitaire intègre, et il existe sur son corps des fractions K une valuation v, à valeurs entières mais non toutes nulles, telle que

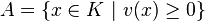
Par conséquent (comme tout anneau d'une valuation non triviale) A est un anneau local mais pas un corps, et son unique idéal maximal M est non nul, et constitué des éléments de valuation strictement positive :

$M=\{x\in K\ |\ v(x)>0\}$ .

De plus (comme la valuation est à valeurs entières) tout idéal est engendré par n'importe lequel de ses éléments de valuation minimum, si bien que A est principal. (Un générateur de M est appelé uniformisante ou paramètre local de l'anneau.)

La réciproque est claire : tout anneau local et principal qui n'est pas un corps est un anneau de valuation discrète (on pose v(a) = l'entier n tel que aA = Mⁿ, cf paragraphe "Propriétés"). On obtient donc une définition équivalente :

Seconde définition — Un anneau de valuation discrète est un anneau principal, qui ne possède qu'un idéal maximal, et tel que cet idéal soit non nul.

Exemples

Un exemple simple est fourni par un sous-anneau de l'ensemble des rationnels : considérons l'ensemble Z_(p) des fractions a/b où a est un entier relatif et b un entier différent de zéro et premier avec un nombre premier p fixé. On vérifie immédiatement que cet ensemble forme un anneau. Tous les éléments de Z_(p) non nuls formés par une fraction ne comportant pas de multiple de p au numérateur (et par définition pas non plus au dénominateur) sont les éléments du groupe des unités (c'est-à-dire le groupe des éléments inversibles de l'anneau).

Une généralisation naturelle est de remplacer Z par un anneau de Dedekind A (par exemple : par la fermeture intégrale de Z dans un corps quadratique ou plus généralement dans un corps de nombres). Soit P un idéal premier non nul de A, le localisé A_P de A en P est un anneau de valuation discrète (c'est l'ensemble des fractions de la forme a/b où a est élément de A, et b un élément de A qui n'est pas dans P).

Critères

Construire un anneau local est relativement aisé : il suffit de considérer localisé d'un anneau commutatif unitaire en un idéal premier. Mais un tel anneau n'est pas toujours principal. Exemple : le localisé de l'anneau des polynômes $Z [X, Y]$ en l'idéal premier $P = < X, Y >$ .

Pour cette raison, il est utile de rechercher des critères permettant d'établir qu'un anneau A est de valuation discrète. La théorie algébrique des nombres utilise en particulier le dernier de cette liste:

Théorème — Soit A un anneau noethérien local, d'idéal maximal M non nul. Les propriétés suivantes sont équivalentes :

les idéaux premiers de A sont (0) et M, et le A/M-espace vectoriel M/M² est de dimension 1,
M est un idéal principal non nilpotent (c'est-à-dire dont toutes les puissances sont non nulles),
les idéaux de A sont (0) et les puissances de M,
A est un anneau de valuation,
A est un anneau de valuation discrète,
A est principal,
A est factoriel,
les idéaux premiers de A sont (0) et M, et A est intégralement clos.

Certaines de ces hypothèses sont évidemment redondantes : l'ajout "noethérien" est superflu dans 3, 5 et 6, de même que l'ajout "local" dans 3, 4, 5 et 8, et l'ajout "M non nul" dans 1, 2 et 5. Remarquons que la condition "A intègre" (qui équivaut à "(0) est premier") n'est pas imposée a priori dans 2, mais sera une conséquence des équivalences.

$6\Rightarrow 1$ étant immédiat, on va démontrer (par une boucle d'implications) que les critères 2 à 8 sont équivalents et que (par exemple) $1\Rightarrow 2$ .

$1\Rightarrow 2$ : Soit $\scriptstyle t\in M\setminus M^2$ , alors M = tA + M ² donc (d'après le lemme de Nakayama) M = tA. Puisque t est non nul (car il n'appartient pas à M²) et que A est intègre, toutes ses puissances sont non nulles donc M n'est pas nilpotent.

$2\Rightarrow 3$ : Aucune des puissances de M n'est nulle, alors que leur intersection l'est (comme dans tout anneau local noethérien). Pour tout idéal non nul I, il existe donc un plus grand entier n tel que I soit inclus dans Mⁿ. Pour cet entier n, (I+ Mⁿ⁺¹) / Mⁿ⁺¹ est un sous-espace non nul du A / M-espace vectoriel Mⁿ / Mⁿ⁺¹. Or cet espace est de dimension au plus 1 (c'est ici qu'on utilise que M est principal), donc le sous-espace non nul lui est égal, c'est-à-dire Mⁿ = I + Mⁿ⁺¹. Par le lemme de Nakayama, on conclut que I = Mⁿ.

$3\Rightarrow 4$ : La condition 3 implique que l'ordre d'inclusion sur les idéaux de A est total, ce qui caractérise les anneaux de valuation.

$4\Rightarrow 5$ : Par noetherianité, M est finiment engendré. Si A est l'anneau d'une valuation v sur K, v(M) possède donc un élément minimum, ce qui assure que v est discrète.

$5\Rightarrow 6$ a déjà été vu ; $6\Rightarrow 7$ et $7\Rightarrow 8$ sont classiques.

$8\Rightarrow 2$ : Soient K le corps des fractions de A et a un élément non nul de M. Il existe un entier naturel n tel que M ⁿ soit inclus dans aA (car dans un anneau noethérien intègre, tout idéal non nul contient un produit d'idéaux premiers non nuls). Choisissons le plus petit n vérifiant cette propriété. Comme a appartient à M, n n'est pas nul ; et comme n est choisi minimal, il existe un élément b de M ^n-1 qui n'est pas élément de aA. Posons k = b / a (élément de K) : alors k n'appartient pas à A donc (puisque A est supposé intégralement clos) k n'est pas entier sur A, donc il n'existe pas de A[k]-module fidèle qui soit de type fini en tant que A-module, si bien que M (qui est un A-module de type fini, comme idéal d'un anneau noethérien) ne peut être stable par produit par k. Ainsi, kM n'est pas inclus dans M. Il est cependant inclus dans A (car bM est inclus dans M ⁿ donc dans aA). C'est donc un idéal de A non inclus dans l'idéal maximal M. Par conséquent, kM = A, donc M = tA pour t = k ⁻¹, si bien que M est principal. (Il est non nilpotent, puisque A est intègre.)

Propriétés

- Introduction - Définitions et exemples - Critères - Propriétés

Des particules de lumière "filmés" dans leur déplacement 🎬

Montre moi tes mains, je te dirai quel buveur d'alcool tu es 🍺

Ces papillons interprètent les "cris" des plantes pour choisir où pondre 🦋

Le nombre d'articles scientifiques rétractés est en hausse ❌

Une nouvelle manière de lire les mémoires magnétiques 🧲

Vous êtes né avant 1986 ? Voici pourquoi vous risquez de développer des troubles psychiques ⚠️

Ce nouveau modèle relie matière noire et inflation cosmique 🌀

Ils ont rendu ce bois bioluminescent: vers un nouveau mode d'éclairage ? 💡

Des mouches dans la station spatiale chinoise Tiangong 🛰️

Cette main-robot nanométrique est capable de saisir des virus (exemple avec la COVID-19) 🖐️

Une étoile dévorée à pleine vitesse par... un trou noir ? 🌟

Cette astuce simple réduit la consommation d'alcool... des femmes 🍷

Découverte: la lumière transforme un isolant en métal 💡

Cet aliment à bannir nourrit les cancers 🍽️

Cette tablette de 3000 ans dévoile une écriture jusqu'alors inconnue ✍️

Découverte d'une chimie des océans refroidissant le climat 🌊

Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭

Le rôle surprenant de la grossesse contre la grippe A 🦠

Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️

Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋

Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬

Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️

Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️

Ce nouveau type de moteur repousse les limites du vol supersonique ✈️

Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠

Une super-Terre entre Mars et Jupiter ? 🌎

Découverte impressionnante d'un fossile de crocodile géant 🐊

Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡

Un virage technologique révèle l'impact du diabète gestationnel 🩺

Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼

Ce fin gilet robotisé soulage les tâches répétitives 🦾

Les équations d'Einstein invalidées ? 👀

Ce tatouage électronique se connecte à votre cerveau 🧠

Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️

Des plats au bœuf... sans bœuf ? 🥩

Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍

Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️

Découverte: d'autres univers plus propices à la vie que le notre 👽

Ces sons urbains qui minent notre santé mentale 🚗

La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥

Des microalgues éliminent les métaux lourds: voici comment 🧪

Et voici un qubit mécanique ! 🖥️

Les lentilles de contact sont-elles vraiment sans danger ? 👁️

Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥

Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠

Cette astuce quotidienne ajoute 11 ans à votre vie 🕒

Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋

Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀

Voici pourquoi l'alcool peut rendre agressif 🥂

Expérience inédite: ce laser projette une ombre visible 💥

Page générée en 0.129 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise