Courbe algébrique - Définition
La liste des auteurs de cet article est disponible ici.
Correspondance entre courbes et corps de fonctions
Pour toute courbe (projective régulière et irréductible), son corps des fonctions rationnelles K(C) est un corps de fonctions d'une variable.
Si
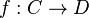
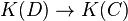
On obtient ainsi un foncteur de la catégorie des courbes projectives régulières irréductibles, dont les morphismes sont les morphismes non-constants de k-schémas, vers la catégorie des corps de fonctions d'une variable, dont les morphismes sont les morphismes de k-extensions.
- Théorème: le foncteur ci-dessus est une équivalence de catégories.
Concrètement, cela veut dire que la donné d'une courbe est équivalente à la donné de son corps de fonctions, et que la dommné de morphismes non-constant est équivalente à la donné d'extensions finies de corps de fonctions.
Note: si k n'est pas parfait, il existe des corps de fonctions d'une variable qui ne soient pas des corps des fonctions rationnelles de courbes projectives lisses irréductibles. En revanche, si k est parfait, il n'y a pas de distinction entre régulier et lisse.
Définition Soit
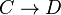
Classification des courbes projectives lisses
Un premier invariant pour distinguer les courbes algébriques entre elles est le genre, qui rappelons-le, est la dimension de l'espace vectoriel des formes différentielles sur la courbe. C'est donc un entier positif ou nul.
Les courbes de petit genre
- On a g(C) = 0 si et seulement si C est une conique (non-dégénérée). Une conique est isomorphe (en tant que variété algébrique) à la droite projective si et seulement si elle possède un point rationnel. Le diviseur canonique sur une courbe de genre 1 est le diviseur nul.
- Si g(C) = 1 et si C a un point rationnel, alors C possède une structure de courbe elliptique. Dans le cas général, la jacobienne J de C est une courbe elliptique et C est un torseur (espace homogène principal) sous J (grosso modo, J opère transitivement et librement sur C).
- Si g(C) = 2, alors C est une courbe hyperelliptique.
- Pour tout
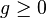
![f(x)\in k[x]](https://static.techno-science.net/illustration/Definitions/autres/5/5b2703f2563ff12348128f782553bbd2_7080df00fa6da61746880592d7400e36.png)
- Les courbes de genre 3 sont soit hyperelliptique sur la clôture algébrique de k, soit une courbe plane de degré 4.
Espace de modules des courbes de genre g
Un espace de modules est une variété algébrique ou plus généralement un schéma dont les points correspondent à une classe d'objects provenant de la géométrie algébrique. Un espace de module est dit fin lorsqu'il représente un foncteur de la catégorie des variétés algébriques dans la catégorie des ensembles.
Fixons le corps de base k et un genre g. On peut considérer l'ensemble Cg des classes d'isomorphes des courbes de genre g sur k. On montre qu'il existe une variété algébrique intègre, normale et quasi-projective Mg sur k tel qu'il existe une application naturelle
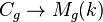
L'espace de modules Mg est dit grossier car il ne représente pas le foncteur des courbes projectives lisses de genre g (lequel foncteur n'est tout simplement pas représentable), mais ses points sur un corps algébriquement clos sont en bijection avec l'ensemble Cg, et la variété est en un sens minimal pour cette propriété.
Notons que contrairement aux surfaces topologiques, ce qui précède dit que le genre (à partir de 1) ne détermine absolument la courbe à isomorphisme près.

















































