Courbe algébrique - Définition
La liste des auteurs de cet article est disponible ici.
Riemann-Roch
Le théorème de Riemann-Roch donne une estimation de la dimension de l'espace des fonctions rationnelles à pôles contrôlés par un diviseur donné. C'est un résultat fondamental dans l'étude des courbes algébriques. Concrètement, on se donne des points
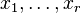
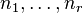
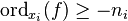
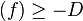
- Si D et D' sont linéairement équivalentes, alors l(D) = l(D').
-
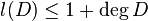
-
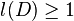
-
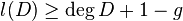
- (Théorème de Riemann-Roch) On a l'égalité
- Corollaire:
-
- on a degK = 2g − 2;
- si degD > 2g − 2, alors l(D) = degD + 1 − g.
Définition Une courbe hyperelliptique est une courbe de genre au moins 2, dont le corps de fonction est une extension (nécessairement séparable) de degré 2 du corps des fractions rationnelles k(x). Cela revient donc à dire que C admet un morphisme de degré 2 vers
Exemples
- Une courbe projective plane donnée par une équation homogène de degré n est de genre (n − 1)(n − 2) / 2.
- Une courbe hyperelliptique correspondante à une extension y2 = f(x) (en caractéristique différente de 2) avec
![f(x)\in k[x]](https://static.techno-science.net/illustration/Definitions/autres/5/5b2703f2563ff12348128f782553bbd2_7080df00fa6da61746880592d7400e36.png)
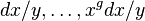
- Sur la droite projective, le diviseur canonique est linéairement équivalent à − 2[x] si x est un point rationnel quelconque.
Plongement dans un espace projectif
- Sur un corps infini, toute courbe projective lisse se plonge dans
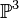
De façon plus canonique:
-
- si g > 2, le diviseur canonique induit un plongement dans
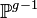
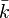
- si g > 2, le diviseur canonique induit un plongement dans
-
- si g > 1, alors 3K (qui correspond à la puissance tensorielle
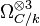
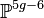
- si g > 1, alors 3K (qui correspond à la puissance tensorielle
Groupe des automorphismes
Tout automorphisme de C se prolonge en un automorphisme de
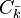
- Le groupe des automorphismes de la droite projective est isomorphisme au groupe des homographies PGL2(k).
- Supposons C de genre 1 et désignons arbitrairement un point x0. Pour éviter les confusions possibles, on va noter par E la courbe elliptique constituée de C avec x0 comme élément neutre. Alors le groupe Aut(C) s'inserre dans une suite exacte
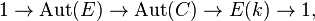
la dernière flèche envoyant un automorphisme σ sur σ(x0). Le groupe Aut(E) est en général le groupe cyclique d'ordre 2, et peut être exceptionnellement cyclique d'ordre 4 ou 6. Si le corps est de caractéristique 2 ou 3, ce groupe peut aussi être d'ordre 12 ou 24.
- Si C est de genre g > 1, alors Aut(C) est un groupe fini. Si de plus, le corps de base est caractéristique nulle, alors l'ordre du groupe est borné par 84(g − 1) = 42degK. En caractérisitique positive cette borne linéaire n'est plus valable. Il faut lui substituer une borne polynomiale du type cg4 avec une constante explicite c de l'ordre de 14x16.
- Si g > 2 et si C est suffisamment générale, alors Aut(C) est trivial. Plus précisément, il existe un ouvert dense U de l'espace de modules Mg tel que la conclusion ci-dessus tienne pour toute courbe induisant un point dans U.

















































