Courbe du dragon - Définition

Introduction

La courbe du dragon (ou "Fractale du dragon" ou "courbe de Heighway" ou "dragon de Heighway") a été pour la première fois étudiée par les physiciens de la NASA John Heighway, Bruce Banks, et William Harter. Elle a été décrite par Martin Gardner dans sa chronique de jeux mathématiques du Scientific American en 1967. Nombre de ses propriétés ont été publiées par Chandler Davis et Donald Knuth. Elle est apparue dans le roman de Michael Crichton Jurassic Park.

Construction

L-system

La courbe peut être construite par L-system avec

• angle 90°
• graine FX
• règles :
  • X X+YF+
  • Y -FX-Y

Ce qui se traduit simplement comme suit: Partir d'un segment de base; puis en suivant la courbe, remplacer chaque segment par deux segments à angle droit en effectuant une rotation de 45° alternativement à droite puis à gauche:

On visualise ici les 5 premières itérations et la neuvième.

IFS

La courbe du dragon est également l'ensemble limite de l'IFS suivant, dans le plan complexe:

.

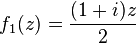
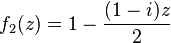
Pliage

Suivre une itération de la courbe du dragon fait apparaître une suite de rotations à 90° vers la droite ou vers la gauche. Pour les premières itérations, la séquence de 'droite' (D) et 'gauche' (G) est la suivante:

1ere itération: D

2eme itération: D D G

3eme itération: D D G D D G G

4eme itération: D D G D D G G D D D G G D G G

Empiriquement, on peut observer la règle de construction suivante : on peut construire l'itération suivante en prenant l'itération en cours, ajoutant un D, puis en ajoutant l'itération courante inversée et en intervertissant D et G.

Ce schéma suggère la méthode suivante de modélisation par pliage: prenez une bande de papier et pliez là en son milieu par la droite. Pliez-la à nouveau par la droite et répétez l'opération autant de fois que possible. Dépliez la bande en conservant les pliures à 90°. La courbe du dragon apparaît.

Ce motif donne également une méthode pour déterminer la direction de la nième rotation dans la séquence. Écrivons « n » sous la forme k2^m où k est un nombre impair. La direction de la nième rotation est déterminée par k modulo 4 (reste de la division de k par 4). Si le reste vaut 1 alors la nième rotation est « droite”, sinon « gauche”.

Variantes de la courbe du dragon

Twindragon

La twindragon (mot à mot « dragon jumeau », connue également sous le nom de dragon de Davis-Knuth) est une variante de la courbe du dragon qui peut être construite en plaçant deux dragons dos à dos. Cette courbe est la limite de l’IFS suivante :

.

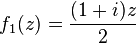
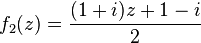
Terdragon

La terdragon peut être construite à partir du L-system suivant:

• angle 120°
• graine F
• règle:
  • F F+F-F

C’est également la limite de l’IFS suivant:

f₁(z) = λz

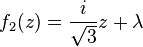
f₃(z) = λz + λ ^*

.

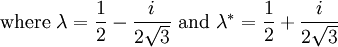
Propriétés de la courbe du dragon

Dimensions

• En dépit de son aspect irrégulier, la courbe du dragon s’inscrit dans des proportions simples. Ces résultats se déduisent de son mode de construction.

• Sa surface vaut ½ (considérant que le segment de base a pour longueur 1). Ce résultat se déduit de ses propriétés de pavage.
• Sa frontière a une longueur infinie.
• La courbe ne se traverse jamais
• La courbe du dragon révèle nombre d’auto-similarités. La plus visible est la répétition du même motif après rotation de 45° et reduction de .

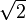
• Sa dimension fractale peut être calculée : A chaque itération le nombre de segments double avec un facteur de réduction de . La dimension fractale vaut donc . Cette courbe couvre donc le plan.
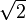
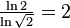
• Sa frontière est une fractale dont la dimension fractale vaut 1,5238 (calculée par Chang & Zhang).

Pavage

• La courbe du dragon peut paver le plan de multiples manières (voir encadré).

1er élément de pavage par 4 courbes	2eme élément de pavage par 4 courbes	3eme élément de pavage par 4 courbes	La courbe du dragon peut se paver elle-même
1er élément de pavage par 2 courbes	2eme élément de pavage par 2 courbes (twin dragon)	3eme élément de pavage par 2 courbes	un exemple de pavage du plan
autre exemple de pavage du plan	autre exemple de pavage du plan	Des courbes de taille croissante (ratio racine(2)) forment une spirale infinie. 4 de ces spirales, disposées à 90°, pavent le plan.